The bolometers have been developed at IAS, and benefitted from studies
in the 40 mK - 150 mK range done for thermal detection of single
events due to X-ray or ![]() sources (Zhou et al. 1993) or to recoil
of dark matter particles (de Bellefon et al. 1996). The design (see
Fig. 7) is that of a classical composite bolometer with a
monolithic sensor as devised by Leblanc et al. (1978). The absorber is
made of a diamond window (3.5 mm diameter and 40 microns thickness)
with a bismuth resistive coating (
sources (Zhou et al. 1993) or to recoil
of dark matter particles (de Bellefon et al. 1996). The design (see
Fig. 7) is that of a classical composite bolometer with a
monolithic sensor as devised by Leblanc et al. (1978). The absorber is
made of a diamond window (3.5 mm diameter and 40 microns thickness)
with a bismuth resistive coating (
![]() )
to match optical
vacuum impedance. The sensors were cut in a selected crystal of NTD Ge
to obtain an impedance around
)
to match optical
vacuum impedance. The sensors were cut in a selected crystal of NTD Ge
to obtain an impedance around
![]() at 150 mK (the
effective temperature of the bolometers during these observations,
because the thermal and atmospheric backgrounds load the bolometers
above the 0.1 K cryostat temperature). The whole sensitive system is
integrated in an integration sphere coupled to the light cone.
Moreover, by using an inclined absorber with a larger diameter than
the 2.5 mm diameter of the output of the light cone we finally
increase the optical absorption efficiency
at 150 mK (the
effective temperature of the bolometers during these observations,
because the thermal and atmospheric backgrounds load the bolometers
above the 0.1 K cryostat temperature). The whole sensitive system is
integrated in an integration sphere coupled to the light cone.
Moreover, by using an inclined absorber with a larger diameter than
the 2.5 mm diameter of the output of the light cone we finally
increase the optical absorption efficiency ![]() from 40 to 80%,
before residual rays go out of the integration sphere (see
Eq. 5). Indeed, the optical efficiency can be estimated
with the well-known Gouffe's formula (Gouffe 1945), by considering
that the effective cavity surface S is twice the surface of the
resistive bismuth coating (which has an emissivity larger than 0.4:
Carli et al. 1981). The entrance surface s is the 2.5 mm diameter
output of the cone. With
S/s= 2 (3.5/2.5)2=3.9, the final cavity
emissivity is larger than 0.8. An additional internal calibration
device (Figs. 7 and 3: a near infrared light
fed by a diode on the back of the bolometer via an optical fibre) was
sucessfully tested but not subsequently used, once the optics was
available.
from 40 to 80%,
before residual rays go out of the integration sphere (see
Eq. 5). Indeed, the optical efficiency can be estimated
with the well-known Gouffe's formula (Gouffe 1945), by considering
that the effective cavity surface S is twice the surface of the
resistive bismuth coating (which has an emissivity larger than 0.4:
Carli et al. 1981). The entrance surface s is the 2.5 mm diameter
output of the cone. With
S/s= 2 (3.5/2.5)2=3.9, the final cavity
emissivity is larger than 0.8. An additional internal calibration
device (Figs. 7 and 3: a near infrared light
fed by a diode on the back of the bolometer via an optical fibre) was
sucessfully tested but not subsequently used, once the optics was
available.
![\begin{figure}
\includegraphics[width=8.8cm,clip]
{ds1696f6.eps} \end{figure}](/articles/aas/full/2000/03/ds1696/Timg25.gif) |
Figure 6: Schematic drawing of the Diabolo open-cycle dilution refrigerator. See Sect. 3. The cold plate is at 100 mK. The lHe is pumped in order to reach a temperature of 1.8 K which is required by the dilution fridge |
The theory of responsivity and noise from a bolometer has been written
by Mather (1984) and Coron (1976). At the equilibrium, the Joule
power dissipated in the bolometer, ![]() ,
and the absorbed radiation
power,
,
and the absorbed radiation
power, ![]() ,
are balanced by the cooling power
,
are balanced by the cooling power ![]() due to the small
thermal link to the base temperature:
due to the small
thermal link to the base temperature:
| (1) |
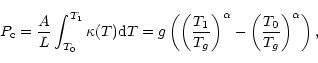 |
(2) |
| (3) |
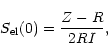 |
(4) |
The bolometer also responds to the base plate temperature fluctuations with a responsivity that can be deduced from the previous formalism:
The time constant is less than 10 milliseconds for both bolometers as measured with particles absorbed by the bolometers against a small radioactive source.
The background is relatively large in the case of ground-based experiments. There is a general prejudice that very low temperatures are thus not needed. Actually, the temperature required for optimised bolometers depends only on the wavelength, because the photon and bolometer noises both increase as the square root of the incoming background. The general formula is (Mather 1984; Griffin 1995; Benoit 1996):
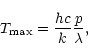 |
(7) |
| (8) |
![\begin{figure}
\includegraphics[angle=90,width=8.8cm]
{ds1696f9.eps} \end{figure}](/articles/aas/full/2000/03/ds1696/Timg62.gif) |
Figure 9:
Mars observed with Diabolo at 1.2 mm at MITO. Contours
are at 20, 40, 60, 80, and 100 mK |
![\begin{figure}
\includegraphics[angle=90,width=8.8cm]
{ds1696f10.eps} \end{figure}](/articles/aas/full/2000/03/ds1696/Timg63.gif) |
Figure 10:
Mars observed with Diabolo at 2.1 mm at MITO. Contours
are at 20, 40, 60, 80, and 100 mK |
![\begin{figure}
\includegraphics[angle=90,width=8.8cm]
{ds1696f11.eps} \end{figure}](/articles/aas/full/2000/03/ds1696/Timg64.gif) |
Figure 11:
Orion observed with Diabolo at 1.2 mm at MITO. Contours
are at 10, 20, 30, 40 mK |
![\begin{figure}
\includegraphics[angle=90,width=8.8cm]
{ds1696f12.eps} \end{figure}](/articles/aas/full/2000/03/ds1696/Timg65.gif) |
Figure 12:
Orion observed with Diabolo at 2.1 mm at MITO. Contours
are at 10, 20, 30, 40 mK |
Copyright The European Southern Observatory (ESO)