4 Results

Altogether, 106 sources were detected with a signal to noise ratio $S/N\geq 3$. In addition to those, in Table 2 we list $2-3\,\sigma$ signals when there are no ISOCAM detections in the field or when they may be associated to an optical source; these data may be used to derive upper limits to ISOCAM-LW3 fluxes of the corresponding IRAS or optical objects. When no $\geq 2\,\sigma$ signal is detected in the field, we give an upper limit equal to 3 times the rms noise of the map at the nominal position of the IRAS source.

In order to assess the reliability of identifications of ISOCAM sources with IRAS sources we have computed, for all ISOCAM sources detected at $\geq 3\sigma$ (less those in the fields 3-19, 3-26, 3-78 and 3-81, where IRAS fluxes may be affected by substantial confusion effects), the mean number of chance objects, $n_{\rm c}$, closer to the nominal position of the IRAS source and brighter than the candidate (Downes et al. 1996):

$$n_{\rm c} = \pi \Delta^2_{\rm IRAS-ISO} N(>S_{14.3~\mu{\rm m}})\ .$$ (1)

In the relevant flux density range ($2-30\,$mJy), the $14.3\,\mu$m integral counts of galaxies are accurately described by (see Elbaz et al. 1999; Aussel 1999; Oliver et al. 1998):

$$N(>S_{14.3~\mu{\rm m}}) \simeq 4.7\ 10^{-2}S_{14.3~\mu{\rm m}}^{-1.34} ({\rm mJy})\ {\rm arcmin}^{-2} \ .$$ (2)

An optimal method for determining the reliability of an identification has been presented by Sutherland & Saunders (1992; see also Wolstencroft et al. 1986). The method, however, requires the prior knowledge of the distribution of $14.3\,\mu$m fluxes which is not available in our case.

Figure 1: Positional differences between IRAS and ISOCAM $(\geq$ $3\sigma )$ sources

As shown by Fig. 1, the center of the distribution of differences between IRAS and ISOCAM positions of ISOCAM sources detected at $\geq 3\sigma$ (excluding the confused fields mentioned above) and with $n_{\rm c} < 5\ 10^{-3}$, that we take as likely counterparts to IRAS sources (the expected number of random coincidences in the full sample is 0.5) is not significantly offset from (0,0). We find:
$\langle \Delta\alpha \cos\delta \rangle = -0\hbox{$.\!\!^{\prime\prime}$ }45 \pm 1\hbox{$.\!\!^{\prime\prime}$ }26$ and $\langle \Delta\delta\rangle = 1.60 \pm 1.38$.

Figure 2: Distribution of angular separations between IRAS and ISOCAM sources

The probability that the ISOCAM counterpart has a positional offset (x,y) from the IRAS source is:

$$f(x,y){\rm d}x\,{\rm d}y = {\exp[- 0.5(x/\sigma_x)^2-0.5(y/\sigma_y)^2] \over 2\pi\sigma_x\sigma_y}{\rm d}x\,{\rm d}y.$$ (3)

The positional error distribution has an approximately circular symmetry (cf. Fig. 1) as expected since the NEPR field was scanned from many different directions (Hacking & Houck 1987). Then, $\sigma_x=\sigma_y=\sigma$ and, in polar coordinates:

$$f(\Delta){\rm d}\Delta = {\exp[- 0.5(\Delta/\sigma)^2] \over \sigma^2}\:\Delta\,{\rm d}\Delta \ .$$ (4)

The distribution of positional offsets, $\Delta$, of ISOCAM sources detected at $\geq 3\sigma$ (excluding confused fields) with respect to IRAS positions can be represented by Eq. (4), with $\sigma = 10\hbox{$.\!\!^{\prime\prime}$ }2$ (see Fig. 2). For comparison, the positional precision of single pointed IRAS observations is $\sim 5''$ in the in-scan direction and $\sim 20''-25''$ in the cross-scan direction (Hacking & Houck 1987); since the NEPR field was scanned from many different directions, the final positional error distribution is much more isotropic and typical values, averaged over all directions will be somewhat larger than $\sim 5''$. As discussed in the previous section, positional errors of our ISOCAM sources are estimated to be $\simeq 3\hbox{$.\!\!^{\prime\prime}$ }25$. Thus the derived rms error of IRAS positions turns out to be $\sim 10''$.

As stressed by Hogg & Turner (1998), flux estimates for faint sources are systematically biased high (in a statistical sense) because in any given observed flux interval there are more sources "brightened'' than "dimmed'' by measurement errors, simply due to the fact that faint sources are more numerous than bright ones.

If $\beta$ is the slope of integral source counts, the maximum likelihood true flux $S_{\rm ML}$ is related to the observed flux $S_{\rm o}$ by (Hogg & Turner 1998):

$${S_{\rm ML} \over S_{\rm o}} = {1\over 2} + {1\over 2} \left(1-{4\beta + 4\over r^2} \right)^{1/2}\ ,$$ (5)

where r is the signal to noise ratio. In the flux density range of interest here $\beta = 1.34$ (cf. Eq. (2)); it follows that there is no maximum likelihood value for $r \leq 3.06$.

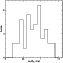Figure 3: Distribution of corrected fluxes, $S_{\rm ML}$, of likely counterparts to IRAS sources ( $n_{\rm c} < 5\ 10^{-3}$) detected at $\geq 5\sigma$

Figure 3 shows the distribution of corrected fluxes, $S_{\rm ML}$, of likely counterparts to IRAS sources ( $n_{\rm c} < 5\ 10^{-3}$) detected at $\geq 5\sigma$.

In addition to sources identified with IRAS targets, we got 10 $\geq 5\sigma$ serendipitous detections with corrected fluxes (see Eq. (5)) $S_{\rm ML} \geq 3.5\,$mJy. The total surveyed area is of $3\hbox{$.\mkern-4mu^\prime$ }2\times 3\hbox{$.\mkern-4mu^\prime$ }2 \times 95 = 973\, \hbox{arcmin}^2$, which, after subtracting the area covered by targets, a few percent, can be rounded to $950\, \hbox{arcmin}^2$. About 20% of pixels are lost because of contamination by cosmic ray hits, leaving a useful area of $\simeq 0.2\,{\rm deg}^2$.

The number of galaxies over this area above $3.5\,$mJy, expected after Eq. (2) is about 6.7. The model by Franceschini et al. (1991) yields $\simeq 8\ 10^{-3}\,{\rm stars}/{\rm arcmin}^{2}$ in the NEPR region ( $l=97^\circ$, $b=30^\circ$), brighter than $5.5\,$mJy at $12\,\mu$m ( $S_{12~\mu{\rm m}} = 5.5\,{\rm mJy}$ corresponds to $S_{14.3~\mu{\rm m}} = 3.5\,{\rm mJy}$ in the case of a Rayleigh-Jeans spectrum peaking at a few $\mu$m), i.e. 7.5 stars in our surveyed area. A slightly higher surface density of stars would be expected based on the results of the deep survey using the LW10 ISOCAM filter, matching the $12\,\mu$m IRAS filter (Clements et al. 1999). These authors found 13 stars brighter than $0.45\,$mJy (after correcting fluxes by a factor 1/1.25, according to the prescription in the caption of their Fig. 5, and by the factor given by Eq. (5)) in an area of $0.1\,{\rm deg}^2$, at high Galactic latitute ( $\langle \vert b\vert \rangle \simeq 54^\circ$), 3 of which are brighter than $5.5\,$mJy. The number of our serendipitous detections is consistent with these results within statistical fluctuations, although a somewhat lower surface density of stars seems to be favoured.

In Table 2 we give: in Col. 1 the target name (HH87), in Cols. 2 and 3 the equatorial coordinates (equinox 2000) of ISOCAM detections, in Col. 4 the position difference (arcsec) between the ISOCAM and IRAS (HH87) sources, in Col. 5 the ISOCAM flux density and its error (mJy), in Col. 6 the maximum likelihood value of the flux density (cf. Eq. (5)) for sources detected at $\geq 5\sigma$, and in Col. 7 the value of $n_{\rm c}$.

Appended to this paper are the finding charts for all ISOCAM detections (Fig. 4). The label on top identifies the field (cf. Table 1); the circle encompasses an area of 45'' radius centered on the nominal position of the IRAS source; the contours are isophotes of the ISOCAM sources. The optical charts are from the Digitized Sky Survey.