4 Properties of the galaxies

4.1 Magnitude and diameter distribution

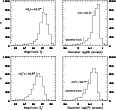
The top panel of Fig. 4 shows the distribution of the observed magnitudes (left) and diameters (right) of the 3279 galaxy candidates identified in the Hydra/Antlia ZOA galaxy search. On average the galaxies are quite small ( $<D> = 21\hbox{$.\!\!^{\prime\prime}$ }8$) and faint (< $B_{\rm J}>$ = 18 $\hbox{$.\!\!^{\rm m}$ }$2).

Figure 4: The distribution of the observed (top panels) and extinction-corrected (bottom) magnitudes (left) and diameters (right) of the 3279 galaxy candidates discovered in the Hydra/Antlia region

However, even the galaxies at the highest latitudes are viewed through an obscuration layer of $A_{B} \approx 1\hbox{$.\!\!^{\rm m}$ }0$ (see Fig. 2) which thickens as we approach the Galactic equator. The observed diameters and magnitudes are heavily influenced by the obscuring effects of the Milky Way. The extinction dims the magnitudes by the amount A_B plus an additional dimming $\Delta$ ( $B_{\rm J}^{\rm o} = B_{\rm J} - A_{ B} - \Delta$) because the observed diameters are reduced, hence also the surface area of a galaxy within the defined isophotal limit.

These obscuration effects on the intrinsic properties of galaxies have been studied in detail by Cameron (1990) who artificially absorbed the intensity profiles of various Virgo galaxies. This led to analytical descriptions of the diameter and isophotal magnitude corrections for early-type and spiral galaxies. For example, a spiral galaxy, seen through an extinction of $A_{B} = 1^{\rm m}$, is reduced to $\sim 80\%$of its unobscured size. Only $\sim 22\%$ of a (spiral) galaxy's original dimension is seen when it is observed through $A_{B} = 3^{\rm m}$. The additional magnitude correction in this case amounts to 1 $\hbox{$.\!\!^{\rm m}$ }$1, a non-negligable amount.

In earlier papers, we used the neutral hydrogen (HI) content in the Milky Way with a constant gas-to-dust ratio as indicator of the foreground extinction. However, the gas-to-dust ratio does vary (e.g., Burstein et al. 1987). Moreover, close to the Galactic plane the Galactic HI line might be saturated, leading to an underestimation of the true extinction. With the recent availability of the 100 micron extinction maps from the DIRBE experiment (Schlegel et al. 1998), we have started implementing these values as they provide a direct measure of the dust column density and the maps have better angular resolution (6 $\hbox{$.\mkern-4mu^\prime$ }$1 compared to $\sim 20-30\hbox{$^\prime$ }$ of the HI maps). Following Cardelli et al. (1989), the Galactic foreground in the blue was determined as

$${A}_{B} = 4.14 \cdot {E(B-V)}.$$ (4)

Applying the Cameron corrections to the observed magnitudes and diameters of the galaxies identified in the ZOA result in a considerable shift of the respective means to $<B_{\rm J}^{\rm o}>$ = $16\hbox{$.\!\!^{\rm m}$ }8$ and $<D^{\rm o}>$ = $34\hbox{$.\!\!^{\prime\prime}$ }7$ (cf., lower panel of Fig. 4). We have avoided unrealistically large extinction-corrections for galaxy candidates in the deepest extinction layers by limiting the maximum correction factors to $A_{B} = 6^{\rm m}$.

A total of 277 galaxies have extinction-corrected diameters larger or equal than $60\hbox{$^{\prime\prime}$ }$, i.e., the Lauberts (1982) diameter limit. This means that in the absence of the obscuration by the Milky Way, Lauberts would have detected 277 galaxies in the ZOA search region instead of the recorded 97 galaxies in his catalog, respectively the 76 galaxies that really have a diameter above $60\hbox{$^{\prime\prime}$ }$. Comparing this to the diameter limit of $1\hbox{$.\mkern-4mu^\prime$ }35$ for which the Lauberts catalog is claimed to be complete (Hudson & Lynden-Bell 1991), 178 galaxies larger than $1\hbox{$.\mkern-4mu^\prime$ }35$ are identified, compared to the 49 galaxies in the Lauberts catalog. These numbers demonstrate the incompleteness in the Lauberts catalog near the plane of the Milky Way. More importantly, it shows the effectiveness of deep optical surveys in retrieving these galaxies.

Figure 5: The observed (top panels) and extinction-corrected (bottom) magnitudes (left) and diameters (right) of the 3279 galaxy candidates discovered in the Hydra/Antlia region as a function of the foreground extinction E(B-V). Some extinction-corrected values fall outside the magnitude/diameter range displayed here

4.2 Dependence on foreground extinction

The effects of the absorption on the observed parameters of these low-latitude galaxies is reflected clearly in Fig. 5. Here, the magnitudes and major diameters are plotted against the Galactic extinction E(B-V) derived from the 100 micron DIRBE/IRAS dust maps. The top panels show the observed magnitudes (left) and diameters (right) and the bottom panels the for extinction corrected parameters.

Figure 6: The cumulative distribution of observed (top panels) and extinction-corrected (bottom) magnitudes (left) and diameters (right) for four different intervals of galactic foreground extinction. The open circles display the galaxies with $A_B \le 1^{\rm m}$, the squares are galaxies with $1^{\rm m} < A_B \le 2^{\rm m}$, the triangles correspond to galaxies with $2^{\rm m} < A_B \le 3^{\rm m}$, and the filled triangles are galaxies with $3^{\rm m} < A_B \le 4^{\rm m}$

The distribution of both the observed magnitudes and diameters show a distinct cut-off as a function of extinction - all the galaxies lie in the lower right triangle of the diagram leaving the upper left triangle empty of points. At low extinction values, bright to faint galaxies, respectively large to small galaxies can be identified, whereas only apparently fainter and smaller galaxies enter our catalog for higher extinction values. The division in the diagram defines an upper envelope of the intrinsically brightest and largest galaxies. This fiducial line, i.e. the shift $\Delta m$ to fainter apparent magnitudes of the intrinisically brightest galaxies, is a direct measure of the absorption A_B. In fact, this shift in magnitude is tightly correlated with the absorption in the blue $A_B = 4.14 \cdot E(B-V)$.

Figure 7: An equal area distribution of all the Lauberts galaxies with extinction-corrected diameters ${D^{\rm o}} \ge 1\hbox {$.\mkern -4mu^\prime $ }$3 in the southern sky ( $\delta \le -17.5{^\circ }$), supplemented with galaxies from our the optical ZOA galaxy search following the same selection criterion. The galaxies are diameter-coded: the galaxies with $1{\hbox {$.\mkern -4mu^\prime $ }}3 \le {D^{\rm o}} < 2\hbox {$^\prime $ }$ are displayed as small, with $2\hbox {$^\prime $ }\le {D^{\rm o}} < 3\hbox {$^\prime $ }$ as middle and the galaxies with ${D^{\rm o}} \ge 3\hbox {$^\prime $ }$ as large circles

In the lower panels of Fig. 5, the for extinction-corrected magnitudes and diameters are plotted as a function of the foreground extinction. Clearly, the faintest galaxies ( ) are only uncovered at the high latitude borders of our survey, whereas the brightest galaxies can still be identified through obscuration layers of ${A}_{B} \approx 4\hbox{$.\!\!^{\rm m}$ }0$. This distribution also has a very well-defined upper envelope which can be used to assess the completeness of the survey as a function of extinction. The distribution indicates that at extinction levels of ${A}_{ B} = 4\hbox{$.\!\!^{\rm m}$ }0$, the survey is complete only for the brighest and largest galaxies ( , ), however at extinction levels of ${A}_{B} = 3\hbox{$.\!\!^{\rm m}$ }0$ we are still complete for galaxies with and , and at extinction levels of ${A}_{ B} = 2\hbox{$.\!\!^{\rm m}$ }0$, for galaxies with or .

4.3 Completeness of the optical survey

A more qualitative assessment of the completeness of our deep optical galaxy survey in the ZOA can be achieved by analysing the cumulative diameter and magnitude distributions (observed and extinction-corrected) as displayed for four different extinction intervals in Fig. 6. The cumulative distribution has not been normalised by the area corresponding to each different interval of galactic extinction. The respective number of galaxies in the extinction intervals are 1089 for $0\hbox{$.\!\!^{\rm m}$ }59 \le {A}_{B} \le 1\hbox{$.\!\!^{\rm m}$ }0$, 1921 for $1\hbox{$.\!\!^{\rm m}$ }0 < {A}_{B} \le 2\hbox{$.\!\!^{\rm m}$ }0$, 218 for $2\hbox{$.\!\!^{\rm m}$ }0 < {A}_{B} \le 3\hbox{$.\!\!^{\rm m}$ }0$ and 37 for $3\hbox{$.\!\!^{\rm m}$ }0 < {A}_{B} \le 4\hbox{$.\!\!^{\rm m}$ }0$.

The slopes of the ${B_{\rm J}} - \log{ N}$ and $\log { D} - \log{ N}$ distributions are slightly lower compared to unobscured regions. With the exception of the bright and large galaxy end of the cumulative distributions and for the highest extinction bin where number counts are low, we find a linear increase of the cumulative curves up to magnitudes of ${B_{\rm J}} = 18\hbox{$.\!\!^{\rm m}$ }5$ and diameters of $\log {D} = 1.15$ ( ${D} = 14\hbox{$^{\prime\prime}$ }$). Then the curves start to flatten. These values hence indicate the completeness limits for the apparent (obscured) parameters of the galaxies of our survey.

The bottom panels of Fig. 6 show the same distributions, but for extinction-corrected magnitudes and diameters. Here, the point at which the curves start to flatten out obviously depends on the amount of foreground extinction. We find that our deep optical galaxy search becomes seriously incomplete only in the interval $3^{\rm m} < A_B \le 4^{\rm m}$ (filled triangles). A detailed analysis based on various extinction bins (not plotted here) finds that we are complete for galaxies and diameters of ( ${ D^{\rm o}} = 60 \hbox{$^{\prime\prime}$ }$) up to extinction levels of ${ A_B} \le 3\hbox{$.\!\!^{\rm m}$ }0$ (the open triangles in Fig. 6).

At ${A}_{B} = 3\hbox{$.\!\!^{\rm m}$ }0$, a spiral galaxy with ${ D^{\rm o}} = 60 \hbox{$^{\prime\prime}$ }$will be visible with ${D} = 14\hbox{$^{\prime\prime}$ }$ only, and an elliptical with ${ D} = 17\hbox{$^{\prime\prime}$ }$. Vice-versa, an obscured spiral or an elliptical galaxy at our apparent completeness limit of ${D} = 14\hbox{$^{\prime\prime}$ }$ would have an intrinsic diameter of ${ D^{\rm o}} \approx 60\hbox{$^{\prime\prime}$ }$, respectively ${ D^{\rm o}} \approx 50\hbox{$^{\prime\prime}$ }$. At extinction levels higher than ${A}_{B} = 3\hbox{$.\!\!^{\rm m}$ }0$, an elliptical galaxy with ${ D^{\rm o}} = 60 \hbox{$^{\prime\prime}$ }$ would appear smaller than the completeness limit ${D} = 14\hbox{$^{\prime\prime}$ }$ of this catalog and might have gone unnoticed. The here presented galaxy catalog should thus be complete for all galaxy types with ${ D}^{\rm o} \ge 60\hbox{$^{\prime\prime}$ }$ down to extinction levels of ${A}_{B} = 3\hbox{$.\!\!^{\rm m}$ }0$. Only intrinsically very large and bright galaxies - particularly galaxies with high surface brightness - will be recovered in deeper extinction layers.

With the above relations between foreground extinction and completeness limit for extinction-corrected galaxies, the first step in arriving at a complete whole-sky survey can be undertaken.

According to Hudson & Lynden-Bell (1991), the Lauberts catalog is complete for galaxies larger than $1\hbox{$.\mkern-4mu^\prime$ }35$. The optical ZOA-survey is complete ${ D}^{\rm o} = 1\hbox{$.\mkern-4mu^\prime$ }0$ at extinction levels of ${ A_B} \le 3\hbox{$.\!\!^{\rm m}$ }0$. Figure 7 combines the two catalogs and shows in an equal-area projection of equatorial coordinates all galaxies with extinction-corrected diameters larger than ${ D}^{\rm o} \ge 1\hbox{$.\mkern-4mu^\prime$ }3$. The Hydra/Antlia ZOA survey region is now filled to Galactic latitudes of (i.e., extinction levels ${ A_B} \le 3\hbox{$.\!\!^{\rm m}$ }0$, cf., Fig. 2). A comparison of Fig. 7 with Fig. 1 demonstrates convincingly how the deep optical galaxy search realizes a considerable reduction of the ZOA. Moreover, the display of the extinction-corrected, diameter-coded galaxy distribution with its well-defined completeness limit clearly reveals the dynamically important large-scale structures of the nearby Universe.

With the other forthcoming optical galaxy searches, we soon will have a much improved consensus about the most important galaxy overdensities in the southern sky.