5 Bulge-disk decomposition

5.1 The model components

Galaxy surface brightness profiles are generally well represented by an exponential disk and a spherical bulge, although bars, ovals, star forming regions and thick disks may cause additional structures (Bahcall & Kylafis [1985]; Bagget et al. [1998] and references therein). The formula for the exponential light profile in flux units is:

$$\begin{array}{lp{0.8\linewidth}} \Sigma(r) = \Sigma_0 \exp (r/h),\\ \end{array}$$

and in magnitudes:

$$\begin{array}{lp{0.8\linewidth}} \mu(r) = \mu_0 \ + \ 1.068r/h, \\ \end{array}$$

where $\Sigma_0$ is the central surface intensity ($\mu_0$ in magnitude units) and h is the scale length. Characteristic for the Freeman type II (Freeman [1970]) profile is that the data dips below the exponential model. In fact, Kormendy ([1977]) first showed that at least empirically the inner-truncated exponential function can better fit this kind of profiles. Recently truncated exponentials have been successfully applied to several spiral galaxies by Bagget et al. ([1998]). Therefore we also used the inner truncated exponential of the form:

$$\begin{array}{lp{0.8\linewidth}} \Sigma(r) = \Sigma_0 \exp \ (-r/h \ - \ (r_h/r)^n), \\ \end{array}$$

where r_h is the radius of the central cutoff of the disk and n=3 as suggested by Kormendy ([1977]).

Successful fits to the bulges of spiral galaxies have been obtained by Hubble law (Hubble [1930]), King model (King [1966]), de Vaucouleurs R^1/4 law (de Vaucouleurs [1948]), by a generalized version of de Vaucouleurs' law R^1/n (Caon et al. [1993]; Andreakis et al. [1995]) and by an exponential function (Kent et al. [1991]; Andreakis & Sanders [1994]; Bagget et al. [1998]). Kormendy has shown that for elliptical galaxies the Hubble, King and R^1/4 models describe approximately the same physical quantities. The most generally used function for bulges is the R^1/4 law, but exponential functions have also been largely applied. In order to better compare with the bulge-disk decompositions presented for spiral galaxies by other authors we applied both the R^1/4 law and the exponential function. The R^1/4 law takes the form of:

$$\begin{array}{lp{0.8\linewidth}} \Sigma(r) = \Sigma_{\rm e} \exp (-7.67 \ [(r/r_{\rm e})^{1/4}-1]), \\ \end{array}$$

$$\begin{array}{lp{0.8\linewidth}} \mu(r) = \mu_{\rm e} \ + \ 8.325 [(r/r_{\rm e})^{1/4}-1], \\ \end{array}$$

where $\Sigma_{\rm e}$ is the effective surface intensity ( $\mu_{\rm e}$ in magnitudes) and $r_{\rm e}$ the effective radius of the bulge.

A less commonly used function to fit the brightness profiles of the bulges, but often used in dynamical galaxy models, is the Plummer sphere with projected surface density

$$\begin{array}{lp{0.8\linewidth}} \Sigma(r) = \Sigma_{\rm p} \ / \ (1+(r/h_{\rm p})^2)^2, \\ \end{array}$$

which was here applied for testing purposes (for Plummer sphere $r_{\rm e} \approx 1.3\ h_{\rm p}$ and $\Sigma_{\rm e} \approx 0.29 \Sigma_{\rm p}$).

5.2 Fitting procedure

Our method of decomposing the bulge and disk components in the luminosity profiles resembles the procedure first advocated by Kormendy ([1977]) and later by Boroson ([1981]). The initial parameters of the profiles are first guessed after which the program iteratively solves the parameter values. The fitting to the data was accomplished by minimizing the weighted rms deviation of the data from the fit:

$$\begin{array}{lp{0.8\linewidth}} \chi^2 = \sum \ w_i \ (\Sigma_i-\Sigma_{\rm fit})^2, \\ \end{array}$$

where $\Sigma_i$ and $\Sigma_{\rm fit}$ denote the measured and modelled surface brightnesses. The main difference to Boroson ([1981]) is that here the fits to the bulge and disk are made simultaneously, rather than attempting to decompose with successive pairwise iterations. The IDL-routine "curfit'' was applied: it uses gradient-expansion algorithm to compose a non-linear least squares fit to a user supplied function. Iterations were performed until the chi-square changed by less than $0.1 \%$.

The weighting function to the data points can be selected either on the purposes to give more weight to the inner portions where the intensities are high or to the lower surface brightnesses describing larger areas, both alternatives being equally well motivated. A commonly used weighting function uses the variance of the intensity measurement as the basis, with the weight of the $i^{\rm th}$ point being:

1. $w_i = 1 / \sigma_i^2$,

where $\sigma_i^2$ is the variance of the $i^{\rm th}$ point (Bevington [1969]). For Poisson statistics $\sigma_i^2 \propto \Sigma_i$ and we use consequently w_i = 1/ $\Sigma_i$. This weighting function has been used for example by Bagget et al. ([1998]) and by de Jong ([1996a]), while in most studies the used weighting function has not been stated.

In order to test the effects of different weighting functions on the bulge and disk parameters three other choices were applied:

$$\begin{array}{lp{0.8\linewidth}} \par 2. \ w_i \ = & constant... ...ar 4. \ w_i = & $1/\Sigma_{\rm annulus}$ , \\ \par\end{array}$$

where $\Sigma_{\rm annulus}$ is the total flux within each measured elliptical annulus in the profile. The first and the third weighting functions give more weight to the lower surface brightnesses, whereas the second and fourth functions stress the inner parts of the profile. We also performed unweighted fits in magnitude units, corresponding to $\chi^2 \ = \ \sum \ (\mu_i-\mu)^2$. The fit performed with the function $w_i \ = \ 1/\Sigma_i^2$ applied to the data in flux units closely corresponds to the fit performed in magnitude units.

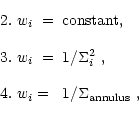
The effects of various weighting functions were studied by running the bulge-disk decomposition routine for a few high quality brightness profiles (NGC 5908 and Arp 87 B) by applying all the above weighting functions. The decomposition routine was first applied to the original data and then to the profiles in which noise ( $10 \% - 30\%$) was added and then the two measurements were compared. The best weighting function, in a sense that it resulted in the smallest variation between the two measurements, was $w_i \ = \ 1/\Sigma_i^2$. While applying the fits to the data in magnitude units without any weighting function, even more stable results were obtained. In this study the last alternative was used.

To account for the effects of seeing the model profiles were convolved with a Gaussian Point Spread Function (PSF) by using the dispersion $\sigma$ measured from the foreground stars for each individual frame (see Table 3, Col. 3). The azimuthally averaged profile, convolved by seeing, can be described as:

$$\Sigma_{\rm s}(r)= \sigma^{-2} \exp (-r^2/2 \sigma^2)$$

$$\ \int \Sigma(x) I_0(xr/\sigma^2) \exp(x^2/2\sigma^2)x{\rm d}x$$

where $\Sigma$(r) is the intrinsic surface brightness profile, $\sigma$ the dispersion of the Gaussian PSF and I₀ the zero-order modified Bessel function of the first kind (Pritchet & Kline [1981]). Eventhough seeing affects most heavily the bulge, our algorithm applies correction also for the disk model functions.

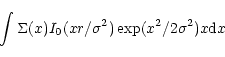
To get an estimate of the goodness of the fit we used the unweighted magnitude residuals:

$$\begin{array}{lp{0.8\linewidth}} \bigtriangleup^2 = \sum \ (\mu_i - \mu_{\rm fit})^2 \ / \ N, \\ \end{array}$$

where $\mu_i$ is the profile value, $\mu_{\rm fit}$ the calculated fitted value and N is the number of data points.

Figure 5: Comparison of the bulge-disk decompositions with different bulge models for Kar 203 B in the V-band: the R1/4 law (deV), Plummer bulge (Plum) and an exponential function (E)

5.3 Fitting the data

The following combinations of the fitting functions were applied:

$$\begin{array}{lp{5.0\linewidth}} 1. & de Vaucouleurs' bulge ... ...\ 5. & Plummer bulge + exp. disk (model 5). \\ \end{array}$$

The models 1 and 2 were applied for most of the galaxies and the resulting parameter values for the bulge and disk are shown in Tables 3 and 4. No corrections for inclination or Galactic or internal extinction were applied. The parameters characterizing the disk are the central surface brightness $\mu_0$, the scale length h and the effective surface brightness and radius $\mu_{\rm e}$ and $r_{\rm e}$ (on the left in the tables), while the bulge is characterized by the effective parameters $\mu_{\rm e}$ and $r_{\rm e}$ (on the right in the tables). Also the resulting bulge-to-disk total flux ratio B/D is shown. Before decomposing the brightness profiles they were generally rebinned outside the bulge regions. Some of the profiles showed strong deviations from exponential disks having bumps above the theoretical profiles. This kind of profiles were fitted by excluding the strong structures. The structures are probably caused by vigorous star formation or by some other component not part of the flat disk, so that excluding them probably made the rms deviations to better reflect quality of the fits to the true disks. We noticed in Sect. 4.2 that some of the profiles were extremely flat in the outer portions. This kind of flat profiles cannot be modelled for example by a second exponential function, because that would cause infinitely large disks. Therefore we decided to exclude the flat outer parts from the profile fits. Some of the images of Arp 296 were saturated in a few nuclear pixels so that the innermost parts of their profiles were excluded from the fit. The decomposition was not applied for NGC 5908 seen almost edge-on, because deprojecting the galaxy to face-on would artificially stretch the spherical bulge.

The bulge-disk decompositions are presented in Fig. 4 so that only the best fitting decompositions, generally in the R-band, are shown. The seeing effect has been discussed in detail by Bagget et al. ([1998]) who pointed out that the errors due to seeing largely depend on the size of the seeing disk compared with the parameters of the fits. According to them the effective radius changes $1 \% - 40 \%$ when seeing has been changed 1-7 arcsecs. In our case, for example, without correcting the 1.5 arcsec seeing observed for Arp 87 B, would cause $10 \%$ error to the effective radius for both the bulge and the disk, $3 \%$ error to the scale length, and less than $1 \%$ error to the central surface brightness of the disk.

5.4 Error analysis

5.4.1 Measurement errors

The most important source of error was the global variations in the sky brightnesses. These uncertainties were estimated by adding the sky level error (estimated as explained in Sect. 4.2) to the original profiles and the measurements were repeated. The differences of the two measurements then gave the errors shown in Table 5. The errors were measured for all profiles, while in the table only the mean values in each band for the two bulge models are shown. As expected, the central and effective surface brightnesses are barely affected, and the uncertainties for the effective radii of the disk are similar for the two bulge models. The errors for the effective radii of the bulge are $5-10\%$ by model 1, while by model 2 they are only half of that. Also, the uncertainties of the B/D ratio are higher when model 1 is applied.

 

 

Table 5: Uncertainties in the derived parameters due to sky variation error

Filter	$\Delta \mu_0$	$\Delta$h	$\Delta m\mu_{\rm e}$	$\Delta \mu_{\rm e}$	$\Delta r_{\rm e}$	$\Delta m\mu_{\rm e}$	$\Delta \mu_{\rm e}$	$\Delta r_{\rm e}$	$\Delta$ (B/D)
model 1
B	0.10	0.35	0.10	0.10	0.43	0.12	0.10	0.88	0.21
V	0.05	0.21	0.07	0.06	0.30	0.12	0.13	0.53	0.13
R	0.04	0.14	0.06	0.04	0.21	0.05	0.06	0.45	0.07
I	0.07	0.27	0.08	0.08	0.51	0.05	0.05	0.46	0.14
model 2
B	0.10	0.57	0.09	0.09	0.74	0.05	0.06	0.13	0.05
V	0.06	0.29	0.06	0.06	0.42	0.07	0.07	0.13	0.01
R	0.03	0.17	0.03	0.05	0.26	0.02	0.04	0.08	0.07
I	0.07	0.32	0.06	0.06	0.47	0.02	0.03	0.07	0.02

 

 

Table 6: Comparison of models 1 and 2 in B-band

Parameter	model 1	model 2
$\mu_0$ (disk)	21.5 $\pm$ 0.7	21.5 $\pm$ 0.7
h (disk)	7.9 $\pm$ 4.3	8.8 $\pm$ 4.2
$m\mu_{\rm e}$ (disk)	21.9 $\pm$ 0.7	21.8 $\pm$ 0.6
$\mu_{\rm e}$ (disk)	23.3 $\pm$ 0.7	23.2 $\pm$ 0.6
$r_{\rm e}$ (disk)	13.0 $\pm$ 7.2	14.3 $\pm$ 6.8
$m\mu_{\rm e}$ (bulge)	21.0 $\pm$ 1.3	19.9 $\pm$ 1.1
$\mu_{\rm e}$ (bulge)	23.0 $\pm$ 1.3	21.3 $\pm$ 1.1
$r_{\rm e}$ (bulge)	6.7 $\pm$ 4.7	2.5 $\pm$ 1.6
B/D	0.9 $\pm$ 0.7	0.3 $\pm$ 0.3

The zero-point errors of the flux calibration were 0.009 - 0.1 mag arcsec^-2 so that their contribution to the bulge and disk parameters are negligible.

5.4.2 Fitting errors

The standard deviations of the fits were considerably smaller than for example the uncertainties due to sky variations. In fact, a more useful way of estimating quality of the fits is to look at the values of the unweighted rms residuals. By taking the mean $\bigtriangleup$ for all the fits performed by one method a quite small mean value $<\bigtriangleup>$ = $0.12 \pm 0.05$ mag was obtained. The bulge model used did not affect the result. Also, while excluding bad fits from the statistics the mean $\bigtriangleup$ was not significantly changed.

The effect of the weighting function to the bulge-disk decomposition has not been previously studied although it may contribute significantly to the uncertainties of the derived parameters. We applied all the weighting functions explained in Sect. 5.2 to the brightness profiles of NGC 5908 and Arp 87 B and compared the measured parameter values to those obtained by the fits made to the unweighted data in magnitude units. For the central surface brightnesses the resulting relative differences were less than $1.5 \%$. However, for the scale lengths the weighting function was more important: depending on the function applied the difference varied between $0.5-20 \%$, and as expected were smallest for the weighting function $w_i \ = \ 1/\Sigma_i^2$.

5.4.3 Comparison of the models

Our third estimate of the decomposition uncertainties was to compare the fits performed by the two bulge models, R^1/4 law and the exponential function. The comparisons in the B-band are shown in Table 6, where the mean parameter values with their standard deviations are shown. In the comparison only those galaxies were used for which good fits were obtained by both bulge models.

It is obvious that changing the bulge fitting model affects mostly the parameters of the bulge, while the parameters of the disk are maintained rather similar. Indeed, mean $r_{\rm e}$ for the bulge was affected even 4.2 arcsec, the fitting model thus being the largest source of uncertainty for this parameter. The bulge model was less important for the parameters of the disk, for example, the central and effective surface brightnesses were hardly affected. The B/D ratio was most dramatically affected, which is well understandable, as the R^1/4 law function extends to a much larger radii than the exponential function. This is demonstrated for Kar 203 B in Fig. 5, where the application of the Plummer bulge is also shown. In fact, the Plummer bulge could for some cases be a very reasonable choice, especially for galaxies with rather large bulges.

5.5 Comparison with previous bulge-disk decompositions

Bulge-disk decompositions for Arp 70 A and B, Kar 64 A and B, and Arp 298 B, common with our sample, have been made by Reshetnikov et al. ([1996]) in the R-band by applying the R^1/4 law for the bulge and an exponential function for the disk. Their fitting method is similar to ours, but contrary to us they did not apply any seeing correction or try elimination of the contributions of the companion galaxies to the brightness profiles. For Arp 298 B the profile by Reshetnikov et al. ([1996]) does not extend to the exponential part of the disk so that comparison was not made. For the galaxies Arp 70 A and B both $\mu_0$ and h for the disk and $\mu_{\rm e}$ for the bulge determined by us were quite different from their values. For example, for Arp 70 A Reshetnikov et al. give $\mu_0 = 23.1$, h = 12.9 and $\mu_{\rm e} = 22.1$, whereas we obtained $\mu_0 = 20.1$, h=5.8 and $\mu_{\rm e} = 21.6$. Evidently the differences, especially for the disk scale length and the central surface brightness, are very large. The reason to the difference is that while Reshetnikov et al. fitted the whole observed profile, we used only the non-flattened part of the profile. We remind that Arp 70 A is one of those galaxies in our sample which has nearly constant surface brightness outside the exponential part of the disk. For Kar 64 A and B our fitting regions were considerably larger than those by Reshetnikov et al. This together with the seeing effect may explain the small differences between the two bulge-disk decompositions. It is also worth noticing that contamination by the light of the companion mainly affects the lower surface brightnesses and therefore can modify the parameters derived for exponential disks.

Bulge-disk decompositions for the galaxies Kar 125 A and Arp 298 A have been performed by Marquez & Moles ([1996]) and by Kotilainen et al. ([1992]), but as their data do not cover the exponential parts of the disks no comparison was made.