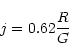 |
(1) |
A code, written in C language to analyse the photon coordinates delivered by the camera, generates two kinds of data set:
Labeyrie (1995) and Boccaletti et al. (1998a, 1998b) have explained how the
dark-speckle method improves the detection of faint structures. It requires fine
sampling to achieve very low light level detection with an optimal value given in
Boccaletti et al. (1998a):
To adjust the sampling with respect to the ratio R/G, the zero-photon events counting
can be made on "big'' pixels containing ![]() or
or ![]() physical pixels. A zero-photon
event is recorded if the photon count is strictly zero in this group of physical
pixels. This process is more efficient than box averaging in this context, and thus
enables to change the pixel sampling on dark-speckle images. Since the detector has
near zero read-out noise, the signal to noise ratio is not degraded through this
operation.
physical pixels. A zero-photon
event is recorded if the photon count is strictly zero in this group of physical
pixels. This process is more efficient than box averaging in this context, and thus
enables to change the pixel sampling on dark-speckle images. Since the detector has
near zero read-out noise, the signal to noise ratio is not degraded through this
operation.
The initial sampling on the camera was therefore set fine enough to allow such grouping
of pixels. Diluting the photon rate also prevents the camera saturation. To avoid a
significant loss of resolution, the groups are kept smaller than ![]() pixels. With
pixels. With ![]() ,
,
![]() and
and ![]() pixels/group, the sampling is then respectively 153, 38.3 and 9.5
pixels/speckle area. The latter is very close to the Shannon sampling.
pixels/group, the sampling is then respectively 153, 38.3 and 9.5
pixels/speckle area. The latter is very close to the Shannon sampling.
The final images are still dominated by the fixed residual speckles, as mentioned in Boccaletti et al. (1998b). These static defects originate in fixed aberrations and from the residual amplitude pattern on the pupil (spider for instance). The coronagraphic images of the binary and the reference stars are recentered and scaled in intensity for subtracting this residual speckle pattern, on both the long-exposure and the dark-speckle image. The map subtraction is quite efficient far from the central star but becomes less effective near the mask, where speckles can be brighter than the hidden companion.
No attempt was made to correct flat-field and dark-current, since they can be neglected at first order, with such a photon-counting camera.
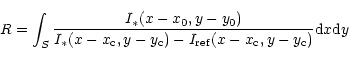 |
(2) |
I*(x-x0,y-y0) is measured on off-axis image where the primary star Airy peak
remains visible while
![]() and
and
![]() are measured on the
on-axis coronagraphic images.
are measured on the
on-axis coronagraphic images.
The subtraction of the PSF halo (
![]() ), measured on the reference star, is needed
for accurate brightness ratio measurement, since in most cases the star halo intensity
is brighter than the companion itself.
), measured on the reference star, is needed
for accurate brightness ratio measurement, since in most cases the star halo intensity
is brighter than the companion itself.
The photometric accuracy with the photon-counting camera is rather poor, owing to the imperfect photon-centroiding (Thiébaut 1994) achieved by the electronics. The photometric accuracy achieved this way is about 0.2 magnitude.
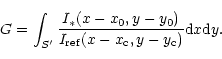 |
(3) |
With the BOA adaptive optics, under good seeing conditions and with moderate pupil
diameter (see Sect. 4), it is therefore possible to reach a gain of about 100-200 at
the companion location (7.6![]() from the Airy peak). A companion about 5
magnitudes fainter than the star will thus be easily detected in a long exposure on
which the speckled halo is smoothed to this intensity level (G). A dark-speckle
analysis imaging is therefore required to improve the detection of fainter companions
(
from the Airy peak). A companion about 5
magnitudes fainter than the star will thus be easily detected in a long exposure on
which the speckled halo is smoothed to this intensity level (G). A dark-speckle
analysis imaging is therefore required to improve the detection of fainter companions
(
![]() ).
).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ds1740_fig1.ps}\end{figure}](/articles/aas/full/2000/01/ds1740/Timg24.gif) |
Figure 1:
Coronagraphic image profiles showing the peak (respectively the dip) of the
companion at position x=124. Long exposure (solid line) and dark-speckle image with
|
Theoretical expressions of the signal-to-noise ratio SNR are:
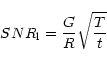 |
(4) |
 |
(5) |
Once the pixels are grouped in ![]() ,
,
![]() or
or ![]() pixels on the dark-speckle exposure, 3 different
pixels on the dark-speckle exposure, 3 different
![]() can be evaluated.
can be evaluated.
| G |
|
|
|
||
| Long exposure | 6.4 | 155 | 87.9 | 53.9 | 27.7 |
| 1 photo-event |
| Sampling |
|
|
|
|
| 6.8 | 31.7 | 78.0 | 28.9 | |
| 30.2 | 59.4 | 175.3 | 51.7 | |
| 107.3 | 97.4 | 314.8 | 80.8 | |
| Theoritical | - | 134.6 | - |
The goal of these laboratory tests was to assess the validity of the dark-speckle model (Boccaletti et al. 1998a), and therefore only the local noise was considered to derive the SNR. Since it does not take into account the residual speckle noise due to static aberrations, this process leads obviously to an optimistic SNR, but more consistent with theoretical expressions.
At the companion location, the SNR is measured over a speckle area (S'), on
both the long exposure and the dark-speckle image, according to the following relation:
 |
(6) |
As explained hereabove, the intensity of the companion's Airy peak on the binary star, is compared to the residual intensity at the same location on the reference star. The noise originating from static aberrations is thus not accounted in the SNR calculation, and a realistic comparison with the model becomes possible.
At this point, it is possible to compare measured (Eq. 6) and expected SNR (Eqs. 4 and 5), separately for the long exposure and
the dark-speckle exposure. But the direct comparison of the dark-speckle and the long exposure efficiency is not straightforward.
The long exposure has positive values and 0 minima while the dark-speckle image is presented in negative form with a maximum value equal to the total
number of frames (Fig. 1). Therefore, dark-speckle images (
![]() in Eq. (7)) have to be scaled to the long exposure, with the following expression:
in Eq. (7)) have to be scaled to the long exposure, with the following expression:
| (7) |
Copyright The European Southern Observatory (ESO)