next previous
Up: Millimeter and some near stars

Subsections

5 Analysis

5.1 Modelling some SEDs

A few very red stars without known pulsation period (all observed with the IRAM-30 m-telescope in December 1994) are treated in a different way from the rest of the sample. The reason is that for some objects no near-IR data and/or pulsation period is available and the methods discussed below could not be applied.

The object OH 10.1-0.1 (IRAS 18052-2016) is located near the galactic centre and thus we assume a distance of 8.0 kpc. The other objects (IRAS 02408+5458, 06582+1507, 05284+1945, 06403-0138, 21554+6204, 22480+6002 = AFGL 2968) are all located outside the solar circle, and were studied by Blommaert et al. (1993). Following Blommaert et al. (1993), kinematic distances could be derived for all objects except IRAS 05284+1945, which in the following we assume to be located at 5 kpc, for otherwise its luminosity would be too low to be on the AGB. Jiang et al. (1997) put this object at 9.8 kpc (for their assumed typical AGB luminosity of 8000 $L_{\odot}$).

As a next step the SEDs and LRS spectra were fitted using the dust radiative transfer model of Groenewegen (1993; also see Groenewegen et al. 1998). IRAS LRS spectra could be retrieved from the database maintained at the University of Calgary (see $\mbox{http://www.iras.ucalgary.ca/$^{\sim}$ volk/\allowbreak getlrs\_plot.html}$), except for IRAS 05284+1945. Broadband data were taken from the IRAS Point Source Catalog (12, 25, 60, 100 $\mu $m data), and IR data from Blommaert et al. (1993) (typically JHKLM and narrow-band data near 10 $\mu $m in the best cases, but note that no near-IR data is available for IRAS 18052-2016 and 21554+6204). For IRAS 05284+1945 a K observation was taken from from Garcia-Lario et al. (1997) and H,K observations from Jiang et al. (1997). For AFGL 2968, I,Kobservations were added from the IRC survey.

The interstellar extinction towards the sources was estimated from the model by Arenou et al. (1992), and ranges from AV = 0.5 - 3.0. For OH 10.1-0.1, probably a Galactic Center source, we assumed an AV of 25. Within the uncertainties, in none of the cases does the adopted value for the extinction influence the derived value for luminosity or dust mass loss rate. The model requires the expansion velocity of the outflow which is taken from the CO measurements.

The resulting fits are displayed in Figs. 10-16. We find two sources to be carbon-rich: IRAS 02408+5458 and 06582 + 1507. This was already suggested by Blommaert et al. (1993) based on the shape of the SEDs, and by Volk et al. (1993) based on the characteristic featureless LRS spectra of very red carbon stars (see also the group V sources in Groenewegen et al. 1992). This is indirectly confirmed here by the good fits obtained with amorphous carbon dust. Both stars lose mass at such high rates that any presence of silicate would result in deep silicate absorption near 10 $\mu $m, which is not observed. The fit to the blue part of the LRS spectrum of IRAS 02408+5458 is not very good however. Recently, Speck et al. (1997) obtained a UKIRT CGS3 8-13$\mu $m spectrum. Their spectrum differs in two ways from the LRS spectrum. First, their spectrum continues to rise to the blue, peaks near 9 $\mu $m and only then drops in flux towards shorter wavelengths, in much better agreement with our model prediction. Second, they find strong silicon carbide absorption at 11 $\mu $m, which is not evident in the LRS spectrum. To simulate this, our model was calculated with 90% amorphous carbon mixed with 10% silicon carbide. The optical depth at 11.3 $\mu $m in our model is 5.5. The differences between UKIRT and LRS spectrum may in part be due to the relatively poor signal-to-noise of the LRS spectrum, but the change from a nearly featureless spectrum to one with strong SiC absorption is real, and suggests an increase in the SiC/amorphous carbon ratio.

Applying the adopted kinematic distances and assuming a dust-to-gas ratio of 0.005, we derive for IRAS 02408 +5458 a luminosity of 5700 $L_{\odot}$ and a mass loss rates of 6.9 10-5 $M_{\odot}$yr-1 and for IRAS 06582+1507 a luminosity of 6500 $L_{\odot}$ and a mass loss rate of 9.0 10-5 $M_{\odot}$yr-1. Note that luminosity and mass loss rate scale with the adopted distance like $L \sim D^2$, and $\dot{M}$ $\sim D$.

The other sources are O-rich, as evidenced by the strong silicate emission or absorption. IRAS 05284+1945, for which no LRS spectrum is available, is an OH (te Lintel Hekkert et al. 1991) and SiO (Jiang et al. 1996) maser source. In all stars except one, a silicate dust opacity was used composed of Jones & Merrill (1976) dirty silicate shortward of 8 $\mu $m, and the silicate of David & Papoular (1990) at longer wavelengths. The exception is IRAS 18052-2016 (OH 10.1-0.1) where, based on the discussion in Suh (1999), we used Mg0.8Fe0.2SiO4 (Dorschner et al. 1995). This was the only silicate out of several species tried which resulted in at least some absorption in the 18 $\mu $m region. However, in view of the still not satisfactory fit of the model to the data, further NIR data is badly needed for this source to confirm if the model prediction for the assumed dust opacity holds at shorter wavelengths. The fits to the SEDs and LRS spectra are quite good, the exception being AFGL 2968 (IRAS 22480+6002). However, taking the kinematic distance, we derive a luminosity of 140 000 $L_{\odot}$, which would make it a supergiant and not an AGB star. In support, its large expansion velocity of 26.4 km s-1 and large 60 $\mu $m flux to T(1-0) ratio (Josselin et al. 1998) are consistent with this interpretation. In fact, Josselin et al. classified it as a M0I object based on unpublished material (Josselin et al., in preparation). This star has not been detected in OH. This is surprising as it is both an SiO (Nyman et al. 1998) and a H2O master source (Han et al. 1998). Possibly the silicate dust opacity around supergiants is different from that typical for O-rich AGB stars, or the dust is more distributed in a disk-like structure. For the other O-sources we find luminosities in the range 1120 to 30 000 $L_{\odot}$, and mass loss rates between 5.0 10-6 and 6.2 10-5 $M_{\odot}$yr-1, again assuming a dust-to-gas ratio of 0.005. The luminosity for IRAS 06403-0138 is quite low (1120 $L_{\odot}$), which might indicate that the kinematic distance is an underestimate of the true distance. Note, again, that luminosity and mass loss rate scale with the adopted distance like $L \sim D^2$, and $\dot{M}$$\sim D$.


   
Table 4: NIR photometry
Name J H K
V390 Cas 6.51 $\pm$ 0.02 5.22 $\pm$ 0.03 4.49 $\pm$ 0.02
PT Cas 6.85 $\pm$ 0.02 5.74 $\pm$ 0.03 5.09 $\pm$ 0.02
AFGL 5076 13.9 $\pm$ 0.3 13.4 $\pm$ 0.1 9.45 $\pm$ 0.03
Y Per 4.63 $\pm$ 0.02 3.68 $\pm$ 0.03 3.25 $\pm$ 0.02
GY Per 6.39 $\pm$ 0.02 5.32 $\pm$ 0.03 4.52 $\pm$ 0.02
C1698 7.66 $\pm$ 0.02 6.51 $\pm$ 0.03 5.78 $\pm$ 0.02
U Ari 2.08 $\pm$ 0.02 1.20 $\pm$ 0.03 0.78 $\pm$ 0.02


  \begin{figure}\par {\psfig{figure=f9.ps,width=8.8cm} } \end{figure} Figure 9: As Fig. 4


  \begin{figure}\par {\psfig{figure=figuur02408.ps,width=8.8cm,angle=-90} } \end{figure} Figure 10: Model fit to the observed SED and LRS spectrum. In the bottom panel the model is the dashed line, the LRS spectrum the solid line. This star is fitted with dust composed of 90% amorphous carbon and 10% silicon carbide


  \begin{figure}{\psfig{figure=figuur05284.ps,width=8.8cm,angle=-90} } \end{figure} Figure 11: As Fig. 10. Silicate dust is used


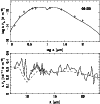  \begin{figure}{\psfig{figure=figuur06403.ps,width=8.8cm,angle=-90} } \end{figure} Figure 12: As Fig. 10. Silicate dust is used


  \begin{figure}{\psfig{figure=figuur06582.ps,width=8.8cm,angle=-90} } \end{figure} Figure 13: As Fig. 10. Pure amorphous carbon dust is used


  \begin{figure}{\psfig{figure=figuur18052.ps,width=8.8cm,angle=-90} } \end{figure} Figure 14: As Fig. 10. Silicate dust is used


  \begin{figure}{\psfig{figure=figuur21554.ps,width=8.8cm,angle=-90} } \end{figure} Figure 15: As Fig. 10. Silicate dust is used


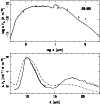  \begin{figure}{\psfig{figure=figuur22480.ps,width=8.8cm,angle=-90} } \end{figure} Figure 16: As Fig. 10. Silicate dust is used

5.2 Luminosity and distance

Luminosities and distances are derived in various ways depending on the amount of available data.

For stars with a pulsation period the luminosity can be derived from a Period-Luminosity (PL) relation. For carbon Miras we use the relation by Groenewegen & Whitelock (1996), which was derived for stars with periods <520 days. This method was used for all carbon stars in the sample, except the five stars with unknown periods. The SEDs of AFGL 5076 and 5625 were fitted by Groenewegen (1995), who assumed a luminosity of 7050 $L_{\odot}$. This is the mean observed for C-stars in the LMC (see e.g. Groenewegen 1999). In the cases of IRAS 02408+5458 and 06582+1507 we refer to the previous section. C1698 is not considered any further as no sensible assumption for its luminosity and distance can be made.

For oxygen-rich Miras we use the PL-relation by Feast et al. (1989) for LMC Miras shifted by the assumed distance modulus of 18.5 (consistent with the procedure in Groenewegen & Whitelock 1996). This was used for 49 out of the 64 O-rich stars in the sample. For the rest of the sample the luminosity was determined by model fitting the SED (AFGL 5093 in Groenewegen et al. 1995, and the objects discussed in Sect. 5.1), or direct integration under the SED (6 stars; Blommaert et al. 1993), with distance estimates either from kinematics (Blommaert et al. 1994), or the "phase-lag'' method (van Langevelde et al. 1990). The distance and luminosity of the S-star W Aql is discussed in Groenewegen & de Jong (1998) based on a comparison with S-stars in the HIPPARCOS catalog.

The SEDs of 25 out of the 35 C-stars were fitted in Groenewegen et al. (1998), two more in Groenewegen (1995), and two in Sect. 5.1 to give the distance for the adopted luminosity. For three stars, we use the Period-MK relation by Groenewegen & Whitelock (1996), together with the observed K magnitudes in Table 4, to derive the distance. For three stars no distance could be derived.

As explained above, for some of the O-rich stars there is a kinematic distance or one from the "phase-lag'' method. For some stars distances were derived by Whitelock et al. (1995) based on a method similar to the one described now.

For most of the stars the distance is derived from the relation between the observed K-band magnitude and MK as given by the P-MK-relation from Feast et al. (1989). No reddening correction are applied, but they should be negligible in the K-band for the distances under consideration here ( $\stackrel{<}{\sim}$1 kpc for the stars this method was applied to). The observed K-band data were preferentially taken from the 2.2 $\mu $m IRC catalog. Observations from Catchpole et al. (1979), Epchtein et al. (1985), Fouqué et al. (1992) and Kerschbaum (private comm.) were also used. No attempt was made to bring these data to a common photometric system.

For 12 out of the sample of 35 C-stars, and 33 of the 62 O-rich stars under consideration a parallax measurement in the HIPPARCOS database (ESA, 1997) is available, but only for 2, respectively 10, objects, has the parallax been determined with an accuracy better than 50%, and only these cases have been included in Table 5. Additionally, for R Leo there is the ground-based parallax determination of Gatewood (1992; $\pi$ = 8.3 $\pm$ 1.0 mas) as well, which is more accurate than the HIPPARCOS parallax. One can compare the distances derived from the HIPPARCOS data and derived from the P-MK-relation. No infrared photometry is available for one star with a HIPPARCOS parallax. In 9 out of 11 cases, the distance based on the P-MK-relation is larger than the HIPPARCOS distance. For the stars with a poorly determined parallax (( $\sigma/\pi) > 0.21$, where $\sigma$ is the error in the observed parallax) this is 7 out of 8. In one case the difference in distance is marginal, but for the other Miras it is a factor of 1.3, and then between factors of 1.9 and 4.4.

A neglect of reddening in our analysis can not be found responsible for this discrepancy. For distances $\stackrel{<}{\sim}$1 kpc, one expects visual extinctions $\stackrel{<}{\sim}$1 magnitude, which translates into AK $\stackrel{<}{\sim}$ 0.1 mag (corresponding to a $\stackrel{<}{\sim}$10% shift in distance). The P-MK-relation was applied to the Galaxy adopting a distance modulus to the LMC of 18.5. A larger distance modulus, as advocated by e.g. Feast & Catchpole (1997), would make the galactic stars only brighter and hence would increase the discrepancy. A possibility is that the LMC is actually closer than adopted here.

A natural explanation for the discrepancy is given by the so-called Lutz-Kelker bias (Lutz & Kelker 1973), and is related to the difference in sampled volume between a star with a parallax between ( $\pi - \sigma$) and ($\pi$), and ($\pi$) and ( $\pi + \sigma$) (also see Oudmaijer et al. 1998). One can introduce the concept of a "most probable parallax'' (e.g. Koen 1992), and its value depends on the underlying distribution of stars and additional constrains one may have (e.g. a luminosity function). In the case of no additional information and an uniform space density the most probable parallax is ( $\frac{1}{2} \pi (1 + \sqrt{1 - 16 (\frac{\sigma}{\pi})^2})$) (Koen 1992). This is defined only for $(\sigma/\pi) < 0.25$. Although perhaps a meaningless comparison for one star only, application of this procedure to R Leo would change the observed HIPPARCOS parallax of 9.87 mas to a probable parallax of 7.62 mas, and the observed ground-based parallax from 8.3 mas to a probable parallax of 7.8 mas, in very good agreement with each other. Based on the "most probable parallax'' for the objects with $(\sigma/\pi) < 0.25$ we adopt the following distances: o Cet (140 pc), R Car (130 pc), and R Leo (130 pc). For the rest of the sample of stars with Hipparcos parallaxes we prefer to use the distance based on the P-MK-relation, because it is more reliable that the distance based on the parallax.


   
Table 5: Derived parameters
 
Name Parallax Lum. D method $v_{\infty}$ ${\dot{M}}_{\rm dust}$ ${\dot{M}}_{\rm gas}$ $\Psi$
  (mas) ($L_{\odot}$) (kpc)   (km s-1) ($M_{\odot}$yr-1) ($M_{\odot}$yr-1)  
V390 Cas   5400 3.10 4b (10) 5.7 10-10 <5.9 10-7 <1035
PT Cas   4400 5.68 4b (10) 0.0 <2.6 10-6 -
CN Per   5720 3.09 1 (10) 1.0 10-9 <4.8 10-7 <480
R For   5790 0.60 1 16.9 4.9 10-9 0. 51-1.9 10-6 204
AFGL 5076   7050 3.99 8 19.7 4.9 10-7 4.1-6.6 10-5 104
IRAS 02408+5458   5700 5.3 9 11.0 3.5 10-7 1.5-1.7 10-5 46
Y Per   3700 1.04 1 7.2 0.0 1.0 10-7 $\infty$
GY Per   5600 3.25 4b (10) 2.6 10-11 <6.2 10-7 <23800
R Ori   5630 2.2 1 10.0 6.0 10-10 3.1 10-7 517
UV Aur   5800 0.85 1 (10) 1.0 10-9 <2.7 10-8 <27
V Aur   5240 1.16 1 20.0 3.0 10-10 4.7 10-7 1570
ZZ Gem   4690 1.32 1 6.9 8.6 10-11 0.76-1.1 10-7 1060
AFGL 935   7430 2.00 1 16.6 2.7 10-8 1.8-6.2 10-6 193
AFGL 971   9910 1.55 1 13.4 4.2 10-8 0.16-1.3 10-5 193
CL Mon   7470 0.82 1 25.3 4.6 10-9 2.1-3.1 10-6 565
IRAS 06582+1507   6500 3.5 9 15.5 4.5 10-7 1.1-4.3 10-5 53
R CMi   5010 0.86 1 (10) 2.0 10-10 <6.4 10-8 <320
R Vol   6800 0.75 1 19.9 1.1 10-8 0.8-2.4 10-6 127
VX Gem   5650 1.62 1 (10) 8.0 10-10 <2.7 10-7 <340
C1698         (10)      
R Pyx   5420 1.20 1 8.8 8.0 10-10 1.8-2.5 10-7 263
V Cru   5600 1.33 1 (10) 3.0 10-10 <4.8 10-7 <1600
V CrB   5310 0.71 1 7.3 1.4 10-9 0.49-2.9 10-7 164
V Oph 3.65 $\pm$ 1.23 4390 0.68 1 7.8 9.5 10-11 3.7-6.7 10-8 526
AFGL 2310   8720 0.81 1 26.0 7.0 10-8 5.1-7.6 10-6 97
AFGL 2368   10280 0.88 1 27.5 8.0 10-8 0.43-1.1 10-5 71
R Cap   5120 1.47 1 9.6 1.0 10-7 1.0-8.0 10-6 27
AFGL 2686   11440 1.08 1 25.2 1.0 10-9 0.76-1.2 10-5 910
V1549 Cyg   8030 1.32 1 15.5 2.0 10-8 4.2-6.1 10-6 275
AX Cep   5890 1.05 1 12.6 4.8 10-9 0.85-1.6 10-6 179
AFGL 5625   7050 1.47 8 18.0 5.8 10-7 0.60-2.2 10-5 20
CIT 13   7050 0.72 1 14.0 1.5 10-8 1.1-3.4 10-6 120
RZ Peg 3.54 $\pm$ 1.36 6570 1.23 1 12.6 5.0 10-10 4.3 10-7 860
AO Lac   4400   4 (10) 8.6 10-11/kpc2 <6.2 10-14/pc2 <720
LS Cas   5000   4 (10) 1.1 10-10/kpc2 <6.2 10-14/pc2 <560
S Scl   6600 0.46 5b 4.5 1.4 10-10 <2.7 10-8 <193
AFGL 230   56 800 2.9 2 12.1 2.5 10-7 3.1-8.9 10-6 29
o Cet 7.79 $\pm$ 1.07 3700 0.14 5a 16.9 4.1 10-9 0.41-2.1 10-6 195
R Cet   2600 0.76 5c 8.7 1.1 10-9 1.3-2.9 10-7 118
R Tri   4600 0.50 5b (10) 2.0 10-10 <1.6 10-8 <80
U Ari   6700 0.76 5b 4.2 2.8 10-10 0.19-1.2 10-7 171
AFGL 5093   15 800 3.2 7 10.3 1.2 10-7 1.7-2.5 10-6 18
AFGL 5097   36 400 6.5 3 12.3 1.4 10-7 4.6-7.2 10-6 41
RT Eri   6700 0.41 5b 7.0 2.9 10-10 2.6-4.1 10-8 114
U Hor   6300 0.94 5b (10) 1.0 10-9 <2.6 10-7 <260
W Eri   6900 0.93 5b 8.6 1.2 10-9 0.81-3.8 10-7 150
RS Eri   5200 0.64 5b 3.4 1.1 10-10 <2.6 10-8 240
R Tau   5700 0.59 5b 5.3 5.4 10-10 1.5-6.5 10-8 39
BD Eri   6000 0.90 5b (10) 6.0 10-10 <4.1 10-7 <680
RX Tau   5900 0.70 5b (10) 6.6 10-10 <5.8 10-8 <88
R Cae   7200 0.50 5b 8.9 5.7 10-10 <9.7 10-8 <170
T Lep   6700 0.43 5c 7.0 5.2 10-10 7.3 10-9 14
NV Aur   5600 1.0 3 18.3 5.2 10-8 0.61-1.2 10-5 152
U Dor   7300 0.76 5c 9.0 2.9 10-9 5.1-6.8 10-7 228
AFGL 712   73 300 8.0 3 13.4 1.4 10-7 2.3-5.2 10-5 250
IRAS 05284+1945   2200 5.0 9 14.0 8.2 10-8 4.7-6.7 10-6 70
RT Lep   7400 0.92 5b 11.9 1.7 10-9 4.4 10-7 260
U Ori   6700 0.31 5b 7.9 7.0 10-10 0.12-2.8 10-7 123
IRAS 06403-0138   1120 2.0 9 10.0 2.5 10-8 3.3 10-7 13
IRAS 07113-2747   35 100 11.0 3 8.1 1.3 10-7 1.4-1.5 10-5 112
AS Pup 3.95 $\pm$ 1.02 5800   5 5.1 8.3 10-10/kpc2 <1.1 10-13/pc2 <133
R Car 7.84 $\pm$ 0.83 5400 0.13 5a 6.8 6.6 10-11 <1.6 10-9 24
X Hya   5300 0.54 5b 6.4 2.9 10-10 2.2-4.8 10-8 110
R LMi   6800 0.29 5b 7.8 4.6 10-10 1.8-5.2 10-8 65
R Leo 9.87 $\pm$ 2.07 5500 0.13 5a 7.3 2.0 10-10 0.35-1.9 10-8 50
W Vel 3.56 $\pm$ 1.69 7300 0.55 5b 6.4 4.6 10-10 <2.3 10-8 <50
RZ Mus   6000 1.11 5b 17.2 3.8 10-9 0.78-2.6 10-6 360
AQ Cen   7100 0.86 5b 10.0 2.4 10-9 3.2 10-7 133


 
Table 5: continued
 
Name Parallax Lum. D method $v_{\infty}$ ${\dot{M}}_{\rm dust}$ ${\dot{M}}_{\rm gas}$ $\Psi$
  (mas) ($L_{\odot}$) (kpc)   (km s-1) ($M_{\odot}$yr-1) ($M_{\odot}$yr-1)  
RU Hya   5900 0.73 5b 7.4 9.7 10-10 1.3 10-7 134
RS Vir   6400 0.74 5b 6.2 1.5 10-9 0.99-3.8 10-7 127
Y Lup   7300 0.67 5b 12.6 1.4 10-9 1.5 10-7 107
S Ser 3.70 $\pm$ 1.62 6800 0.79 5b 8.8 8.6 10-10 <2.2 10-7 <256
RS Lib   3600 0.22 5b 5.0 8.2 10-11 1.8 10-8 220
BG Ser   2200 0.24 5 11.0 2.0 10-10 <2.8 10-6 <14 400
R Ser 3.58 $\pm$ 1.51 6500 0.37 5b 5.8 2.1 10-10 0.14-1.0 10-7 330
RR Sco 2.84 $\pm$ 1.30 4900 0.28 5b 4.2 1.0 10-10 1.1 10-8 110
RW Sco   7200 0.70 5b 10.7 2.4 10-10 2.1-2.2 10-7 875
V545 Oph   3700   5 9.3 1.9 10-9/kpc2 2.1 10-13/pc2 111
V438 Sco   7200 0.87 5b (10) 8.3 10-10 <1.6 10-7 193
WY Her   6900 1.53 5b 10.8 4.5 10-9 1.1 10-6 244
OH 10.1-0.1   30 000 8.0 9 27.3 3.1 10-7 <6.0 10-5 <194
X Oph   5900 0.23 5b 6.3 1.7 10-10 1.6-1.7 10-8 94
V342 Sgr   6800 0.67 5b 15.1 8.0 10-9 1.5-2.4 10-6 250
W Aql   10 380 0.68 6 18.0 2.1 10-8 0.68-2.4 10-5 571
RT Aql   5800 0.67 5b 6.6 6.5 10-10 0.83-2.1 10-7 277
BG Cyg 3.96 $\pm$ 1.41 7900 0.77 5b 5.0 2.1 10-10 7.4 10-8 350
RR Sgr   6000 0.51 5b 5.4 2.8 10-10 5.4 10-8 193
RR Aql   7300 0.55 5b 8.5 2.1 10-9 2.1-6.0 10-7 185
Z Cyg   4500 0.94 5b 4.3 1.8 10-9 0.37-1.8 10-7 78
RU Cap   6300 1.42 5c 7.5 1.9 10-9 3.8 10-7 200
TU Peg   5700 0.63 5b 8.0 4.3 10-10 8.4 10-8 195
IRAS 21554+6204   7560 2.5 9 16.6 2.5 10-7 1.0-2.8 10-5 72
AFGL 2885   27 400 2.30 2 16.5 1.4 10-7 2.2-5.7 10-6 27
AFGL 2968   140 000 5.0 9 26.4 1.4 10-7 1.4-7.2 10-5 350
R Peg   6900 0.46 5b 6.3 3.7 10-10 1.3-8.0 10-8 151
W Peg 3.46 $\pm$ 1.38 6200 0.31 5b 8.0 3.0 10-10 6.1-7.6 10-8 253
R Aqr   7100 0.23 5b 16.7 1.1 10-9 8.7 10-9 7.9

Methods:

1) Luminosity from the C-star PL-relation of Groenewegen & Whitelock (1996). Distance obtained from detailed modelling of the SED (Groenewegen et al. 1998).

2) Distance from the "phase-lag'' method (van Langevelde et al. 1990), luminosity from Blommaert et al. (1994), based on integration under the SED.

3) Distance from kinematics (Blommaert et al. 1994) and luminosity by the same authors, based on integration under the SED.

4) Luminosity from the C-stars PL-relation of Groenewegen & Whitelock (1996); 4b) distance from the observed K-band magnitude and a Period-MK relation (Groenewegen & Whitelock 1996).

5) Luminosity from the PL-relation (Feast et al. 1989) of O-rich Miras in the LMC for a distance modulus of 18.5. Distance from: (5a) most probable parallax (see text); (5b) from the observed K-band magnitude and a Period-MK relation (Feast et al. 1989); (5c) as quoted by Whitelock et al. (1995).

6) From Groenewegen & de Jong (1998).

7) Distance from the "phase-lag'' method (van Langevelde et al. 1990), luminosity scaled from Groenewegen et al. (1995) based on model fitting of the SED. The dust mass loss rate is also derived from the model fitting, appropriately scaled from Groenewegen et al. (1995).

8) Luminosity adopted, distance and dust mass loss rate from model fitting to the SED (Groenewegen 1995), scaled to the adopted velocity.

9) Distance from kinematics (or adopted for IRAS 05285+1945; OH 10.1-0.1 assumed to be near the galactic center at 8.0 kpc), luminosity and dust mass loss from model fitting of the SED (this paper, Sect. 5.1).


5.3 The gas mass loss rate from CO

Olofsson et al. (1993) give the following relation between the measured peak intensity of a CO line and the mass loss rate:

\begin{displaymath}{\dot{M}}_{\rm g} = 1.4 \times \frac{T_{\rm mb} \, v^2_{\infty} \, D^2 \, B^2}{2 \ 10^{19} \, f_{\rm CO}^{0.85} \, s(J)} \end{displaymath} (1)

where ${\dot{M}}_{\rm g}$ is in units of solar masses per year, $T_{\rm mb}$ in Kelvin, $v_{\infty}$ in km s-1, D the distance in parsec. B the FWHM size of the telescope beam in arcsec, $f_{\rm CO}$ the CO abundance relative to H2, and s(J) is a correction factor, equal to unity for the J = 1-0 transition and 0.6 for the J = 2-1 transition.

Equation (1) was calibrated for J = 2-1 and 1-0 transition but in view of the increasing number of available J = 3-2 observations, determination of s(3) would be useful. This was done on the basis of (rewriting Eq. (1) for given stellar parameters):

\begin{displaymath}s(3) = s(2) \left( \frac{ T_{3-2} }{ T_{2-1} }\right)\, \left( \frac{ B_{3-2} }{ B_{2-1} }\right)^2 \end{displaymath} (2)

and only simultaneous observations with the same telescope were used in its application. Based on three stars observed with the CSO by Knapp et al. (1998) a geometric mean of s(3) = 0.43 is derived. Based on our own JCMT data for 7 stars we find s(3) = 0.43, and our own IRAM data on 6 stars results in s(3) = 0.24. The latter value is clearly off, and indicates a possible calibration error (a beam efficiency which is lower), or a contribution from the error beam. If the latter is true it should be less of a problem with the smaller JCMT and CSO telescopes. The IRAM J=3-2 data is not used to make an estimate of the mass loss rate, and in the other cases s(3) = 0.43 is used.

The gas mass loss rate is derived using both our CO results and the CO data in the papers listed in Table 1. Equation (1) was used with $f_{\rm CO}$ = 5 10-4 for O-rich stars and 8 10-4 for C-stars to calculate the mass loss rate per unit distance. The gas mass loss rate listed in Table 5 is the range between minimum and maximum value in the case of multiple determinations.

The expansion velocity is required in this calculation and the finally adopted values are listed in Table 5. They are an average of the available CO data (ours and literature). When no, or only poor, CO data was available the expansion velocity is taken from OH and SiO data, when available, without any correction for the possible difference between the CO and OH/SiO expansion velocity. In other cases a value of 10 km s-1 is adopted.

5.4 The dust mass loss rate

The dust mass loss rate can be derived from a detailed modelling of the SED. This was done for most of the carbon-rich Miras in Groenewegen et al. (1998). In those cases the values they derived from the fit (their Table 3) have been used, appropriately scaled for the slightly different velocities adopted in some cases. The same was done for AFGL 5076 and 5625 (Groenewegen 1995), and AFGL 5093 (Groenewegen et al. 1995), and the stars analysed in Sect. 5.1.

For the rest of the sample the relation between the 60 (or 25) $\mu $m flux and the dust mass loss rate is used. From Jura (1988) we have:

\begin{displaymath}{\dot{M}}_{\rm d} = C \, v_{15} \, D^2 \, L_{4}^{-0.5} {\lambda}_{10}^{0.5} \, {\kappa}_{150}^{-1}\, F(\lambda) \end{displaymath} (3)

where ${\dot{M}}_{\rm d}$ is the dust mass loss rate in units of solar masses per year, C is a constant, v15 is the dust expansion velocity in units of 15 km s-1, D the distance in kpc, L4 the luminosity in units of 10 000 $L_{\odot}$, ${\lambda}_{10}$ the wavelength in units of 10 $\mu $m where the peak of the energy distribution occurs, and ${\kappa}_{150}$ the opacity at 60 $\mu $m in units of 150 cm2 g-1. $F({\lambda}$) is the excess emission at wavelength $\lambda$ in Jansky. Jura (1988) uses C = 7.7 10-10and $\lambda$ = 60 $\mu $m.

It is clear that the excess emission should be used in Eq. (2), but in many applications, the observed flux has been used (see the discussion in Groenewegen & de Jong 1998). Following that paper we have corrected for the photospheric contribution to the observed flux based on a simple radiative transfer model. This correction is explained for O-rich stars in Groenewegen & de Jong (1998; their Fig. 4). In the case of carbon stars we performed similar calculations, which are based on a dust shell composed of amorphous carbon mixed with 10% silicon carbide around a central star with a blackbody temperature of 2500 K. The inner dust temperature was set at 1200 K. Shells of increasing optical depth were calculated and the fraction of excess emission determined as a function of S12/S25 ratio (see Fig. 17).

The constant C in Eq. (3) at $\lambda$ = 60 $\mu $m is 1.34 10-9 for O-rich star models (Groenewegen & de Jong 1998) and 5.35 10-10 for C-star models. At $\lambda$ = 25 $\mu $m these numbers are 2.43 10-10 and 1.49 10-10, respectively[*].


  \begin{figure}{\psfig{figure=f10.ps,width=8.8cm,angle=-90} } \end{figure} Figure 17: Fraction of excess emission at 60 $\mu $m, as a function of flux-ratio at 12 and 25 $\mu $m, for the model described in Sect. 5.4

next previous
Up: Millimeter and some near stars

Copyright The European Southern Observatory (ESO)