

Up: Extraction of a deterministic
![\begin{figure}\includegraphics[width=12cm]{h150912.eps} \end{figure}](/articles/aas/full/1999/19/h1509/Timg51.gif) |
Figure 12:
Short time scale part (t < 16 s) of the time scale spectrum of
the X-ray pulsar 1E2259+586, ROR 400314. Vertical lines indicate
position of different time scale components shown in Table 1.
The logarithm of the time scale is displayed on the x-axis |
![\begin{figure}\includegraphics[width=12cm]{h150913.eps} \end{figure}](/articles/aas/full/1999/19/h1509/Timg52.gif) |
Figure 13:
An amplitude distribution graph for the ampligram in Fig. 8.
(ROR 701246). The horizontal scale shows the normalized amplitude,
vertical scale shows fraction of the maximum wavelet coefficient
magnitude and the color scale shows the logarithm of the relative
occurrence frequency |
![\begin{figure}\includegraphics[width=12cm]{h150914.eps} \end{figure}](/articles/aas/full/1999/19/h1509/Timg53.gif) |
Figure 14:
The distribution entropy as a of the fraction of the maximum
wavelet coefficient magnitude for the distribution graph
of Fig. 13 |
A complementary information may be obtained from the ampligram constructing a
set of amplitude distributions of yl(ti), one for
each level l of wavelet coefficient magnitude. For levels with pure stochastic
component, Gaussian amplitude distributions will be obtained. For levels with
deterministic components, broader amplitude distributions, often revealing
structures, will be found. An example of distribution plot for ROSAT,
ROR 701246 is shown in Fig. 13. In order to enhance sides of the
distributions a logarithmic probability density scale is used.
The amplitudes used to construct the graph in Fig. 13 are normalized to the maximum
value of yl(ti) for each l.
It may be seen that for
wavelet coefficient magnitudes between 0.02 and 0.16 the distribution is
broadened, which is in agreement with the part of ampligram where deterministic
structures may be seen.
A useful method to quantify the above observation is to calculate the
distribution entropy for each level of wavelet coefficient magnitude.
The distribution entropy, El, is calculated as:
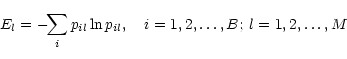 |
(11) |
where pil is the measured probability density, B is number of
distribution bins (100 in our case), and L=20 for a low-20 ampligram.
The entropy for the amplitude distribution pictured in Fig. 13
is shown in Fig. 14.
It may be seen that the broadened distribution corresponds to an increase of
entropy. However, it must be remembered that distinct multiple peaks, if
such appear in the distribution, will again decrease the entropy. That is
illustrated in Fig. 15.
![\begin{figure}\begin{tabular}{ccc}
\includegraphics[width=6cm]{h150915a.eps} &
...
...915b.eps} &
\includegraphics[width=6cm]{h150915c.eps}\end{tabular} \end{figure}](/articles/aas/full/1999/19/h1509/Timg55.gif) |
Figure 15:
The distribution shape and the value of entropy:
a) pure Gaussian noise, narrow distribution, low entropy;
b) the distribution broadened due to presence of semi-regular
components with different periods, increased entropy;
c) strong harmonic component in the data, decreased entropy |
The distribution entropy will be used in the present study as a measure of
occurrence of deterministic structures.


Up: Extraction of a deterministic
Copyright The European Southern Observatory (ESO)
![\begin{figure}\includegraphics[width=12cm]{h150912.eps} \end{figure}](/articles/aas/full/1999/19/h1509/Timg51.gif)
![\begin{figure}\includegraphics[width=12cm]{h150913.eps} \end{figure}](/articles/aas/full/1999/19/h1509/Timg52.gif)
![\begin{figure}\includegraphics[width=12cm]{h150914.eps} \end{figure}](/articles/aas/full/1999/19/h1509/Timg53.gif)
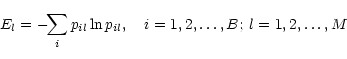
![\begin{figure}\begin{tabular}{ccc}
\includegraphics[width=6cm]{h150915a.eps} &
...
...915b.eps} &
\includegraphics[width=6cm]{h150915c.eps}\end{tabular} \end{figure}](/articles/aas/full/1999/19/h1509/Timg55.gif)