![\begin{figure}
\includegraphics[width=8.8cm,clip]{1410f3.eps}\end{figure}](/articles/aas/full/1999/18/h1410/Timg17.gif) |
Figure 3:
Population change of the
|
![\begin{figure}
\includegraphics[width=8.8cm,clip]{1410f3.eps}\end{figure}](/articles/aas/full/1999/18/h1410/Timg17.gif) |
Figure 3:
Population change of the
|
![\begin{figure}
\includegraphics[width=8.8cm,clip]{1410f4.eps}\end{figure}](/articles/aas/full/1999/18/h1410/Timg18.gif) |
Figure 4:
Population change of the
|
The relative population change of the LIF signal was measured as a function of
the stimulating microwave frequency.
Figure 3 shows the
![]() line together with the
line together with the
![]() line.
Figure 4 shows the
line.
Figure 4 shows the
![]() line together with the
line together with the
![]() line.
The incoupled microwave power was +6.5 dBm which leads to saturation in the main lines and in the
satellite lines.
The interaction time between the OH molecules
and the microwave field is given by the delay between the OH production by the VUV-laser and
the detection by the LIF excitation which terminates the interaction relevant for the results.
The interaction time was 10
line.
The incoupled microwave power was +6.5 dBm which leads to saturation in the main lines and in the
satellite lines.
The interaction time between the OH molecules
and the microwave field is given by the delay between the OH production by the VUV-laser and
the detection by the LIF excitation which terminates the interaction relevant for the results.
The interaction time was 10 ![]() s.
Because of the higher dipole transition moment
the main lines show a stronger saturation broadening than the satellite lines. The fitting includes
saturation broadening, Doppler broadening and lifetime broadening (Wurps et al. 1996).
s.
Because of the higher dipole transition moment
the main lines show a stronger saturation broadening than the satellite lines. The fitting includes
saturation broadening, Doppler broadening and lifetime broadening (Wurps et al. 1996).
The LIF excitation does not resolve the hyperfine splitting of the ![]() -doublet states.
Nevertheless it is possible to calculate the population be the relative population change between th
-doublet states.
Nevertheless it is possible to calculate the population be the relative population change between th
![]() -doublets.
Thus the observable which is dealt with is the relative population change of the
upper
-doublets.
Thus the observable which is dealt with is the relative population change of the
upper ![]() -doublet in case of an interaction of the ensemble of OH fragments with
microwave radiation of the
-doublet in case of an interaction of the ensemble of OH fragments with
microwave radiation of the
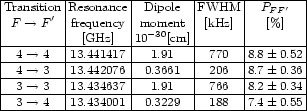
![]() transition (PFF'). The measured PFF' are
shown in Table 1. The PFF' are given by
transition (PFF'). The measured PFF' are
shown in Table 1. The PFF' are given by
with NF being the population of each magnetic state of the
hyperfine levels,
[x]=2x+1 the multiplicity of each hyperfine level and c a constant factor.
In the case of saturated microwave
stimulation the population of the magnetic states of the two coupled hyperfine levels are
equalised. In our example the N3 is equal N4'. The population of the upper F=3 hyperfine
level after stimulation (
![]() )
is then given by
)
is then given by
![\begin{displaymath}N_3^{{\rm stim}}=\frac{N_3[3]+N_{4'}[4']}{[3]+[4']}.
\end{displaymath}](/articles/aas/full/1999/18/h1410/img29.gif) |
(3) |
| S34' | = | (4) | |
| = | ![$\displaystyle c \times\left(N_4[4]+\frac{N_3[3]+N_{4'}[4']}{[3]+[4']}[3]\right)\cdot$](/articles/aas/full/1999/18/h1410/img31.gif) |
(5) |
![\begin{displaymath}P_{FF'}=\frac{[F][F']}{[F]+[F']}\ \frac{\left(N_F-N_{F'}\right)}{N_4[4]+N_3[3]}\cdot
\end{displaymath}](/articles/aas/full/1999/18/h1410/img34.gif) |
(8) |
 |
| |
hyperfine level F |
measured distribution [%] NF[F] |
statistical distribution[%] |
| upper | F=4 |
|
56.25 |
| F=3 |
|
43.75 | |
| lower | F=4 |
|
56.25 |
| F=3 |
|
43.75 |
Copyright The European Southern Observatory (ESO)