8 Appendix A: Entropy derivatives

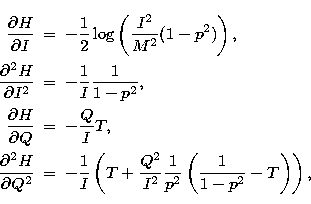
As the maximization process is achieved using a Newton-Raphson iteration, we must evaluate the first- and second-order derivatives of the objective function with respect to pixel values and Lagrange multipliers. For the joint entropy measure,

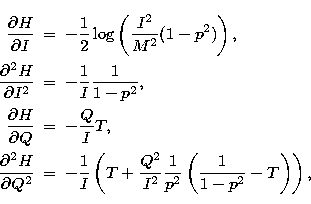$$\begin{eqnarray} \frac{\partial H}{\partial I} &=& -\frac{1}{2}\log\left(\frac{I... ...rac{Q^2}{I^2}\frac{1}{p^2}\left(\frac{1}{1-p^2} - T\right)\right),\end{eqnarray}$$ (A1) (A2) (A3) (A4)

where

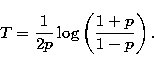$$\begin{eqnarray} T = \frac{1}{2p}\log\left(\frac{1+p}{1-p}\right).\end{eqnarray}$$ (A5)

Derivatives in U and V are similar. As p approaches 0, we use the following limits for the polarized derivatives:

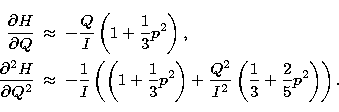$$\begin{eqnarray} \frac{\partial H}{\partial Q} &\approx&-\frac{Q}{I} \left(1+\fr... ... \frac{Q^2}{I^2}\left(\frac{1}{3} + \frac{2}{5}p^2\right)\right).\end{eqnarray}$$ (A6) (A7)