The spectroscopic study of the blue and near-UV region around
![]() 4000 Å has proven to be a useful tool to investigate the
stellar populations of composite stellar systems. Obviously, this
spectral region is specially suited to detect the presence of young
stars and therefore, to study star formation histories. Furthermore,
in a pioneering work, [40, Morgan (1959)] already showed that the
difference in intensity of the continuum level on the two sides of
H
4000 Å has proven to be a useful tool to investigate the
stellar populations of composite stellar systems. Obviously, this
spectral region is specially suited to detect the presence of young
stars and therefore, to study star formation histories. Furthermore,
in a pioneering work, [40, Morgan (1959)] already showed that the
difference in intensity of the continuum level on the two sides of
H![]() (
(![]() Å) in galactic globular clusters correlated
well with metal abundance.
Å) in galactic globular clusters correlated
well with metal abundance.
Although different absorption line-strength indices have been defined
in this spectral range to understand the stellar composition of
early-type objects (e.g., [22, Faber 1973]; [7, Burstein et
al. 1984]; [48, Rose 1984, 1994]; [58, Tripicco 1989];
[67, Worthey et al. 1994], hereafter W94; [32, Jones & Worthey
1995]; [66, Worthey & Ottaviani 1997]; [62, Vazdekis & Arimoto
1999)], some of them are quite dependent on spectral resolution (and
therefore velocity dispersion) and, in many cases, their use requires
relatively high signal-to-noise ratios. In this sense, an interesting
spectral index that avoids these problems is the ![]() 4000 Å break. We have already demonstrated [14, (Cardiel et al. 1998b)] that this
discontinuity can be measured with a relative error of
4000 Å break. We have already demonstrated [14, (Cardiel et al. 1998b)] that this
discontinuity can be measured with a relative error of ![]() %
with a signal-to-noise ratio per
Å
%
with a signal-to-noise ratio per
Å ![]() . Thus, the break is well suited to be measured in faint objects
or at low surface brightnesses. However, this advantage, due to the large
wavelength interval employed in its definition, also translates into an
important drawback: many absorption lines are included in the break
bandpasses. Therefore, the behaviour of the break is expected to be
complex.
. Thus, the break is well suited to be measured in faint objects
or at low surface brightnesses. However, this advantage, due to the large
wavelength interval employed in its definition, also translates into an
important drawback: many absorption lines are included in the break
bandpasses. Therefore, the behaviour of the break is expected to be
complex.
In this work we are using the definition adopted by [5, Bruzual
(1983)], who defined this spectral index as the ratio of the
average flux density, ![]() (erg s-1 cm-2 Hz-1), in
two bands at the long- and short-wavelength side of the
(erg s-1 cm-2 Hz-1), in
two bands at the long- and short-wavelength side of the
![]() 4000 Å discontinuity, in particular
4000 Å discontinuity, in particular
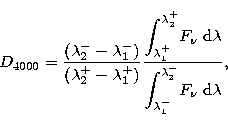 |
(1) |
| (2) |
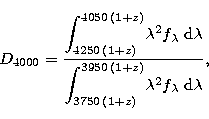 |
(3) |
Up to date, many authors have employed the D4000 to study the stellar composition and star formation history of early-type galaxies (e.g. [38, McClure & van den Bergh 1968]; [54, Spinrad 1980, 1986]; [5, Bruzual 1983]; [35, Laurikainen & Jaakkola 1985]; [28, Hamilton 1985]; [19, Dressler 1987]; [21, Dressler & Shectman 1987]; [31, Johnstone et al. 1987]; [33, Kimble et al. 1989]; [20, Dressler & Gunn 1990]; [47, Rakos et al. 1991]; [16, Charlot et al. 1993]; [15, Charlot & Silk 1994]; [17, Davidge & Clark 1994]; [52, Songaila et al. 1994]; [3, Belloni et al. 1995]; [18, Davidge & Grinder 1995]; [12, Cardiel et al. 1995, 1998]; [1, Abraham et al. 1996]; [29, Hammer et al. 1997]; [2, Barbaro & Poggianti 1997]; [36, Longhetti et al. 1998]; [46, Ponder et al. 1998)]. The reliable analysis of the break measurements rests on the comparison of the data with the predictions of stellar population models (e.g. [65, Worthey 1994]; [6, Bruzual & Charlot 1996)]. So far, such predictions are computed by using either model atmospheres, or stellar libraries with a poor coverage of the atmospheric parameter space, especially in metallicity.
![\begin{figure}
\resizebox {\hsize}{!}{\includegraphics[angle=-90]{ds1707f1.eps}}\end{figure}](/articles/aas/full/1999/16/ds1707/Timg14.gif) |
Figure1:
Spectrum of the star HD 72324 (G9 III) in the region around
the |
In this paper we present an empirical calibration of the
![]() 4000 Å break as a function of the main atmospheric stellar
parameters (namely effective temperature, surface gravity and
metallicity) in an ample stellar library which covers an appropriate
range of parameters to study relatively old stellar populations. One
of the main advantages of using fitting functions to describe the
behaviour of spectral indices is that they allow stellar population
models to include the contribution of all the required stars, through
a smooth interpolation in the space defined by the fitted stellar
parameters. The usefulness of this approach has been demonstrated by
the successful inclusion of similar fitting functions in recent
evolutionary synthesis models (e.g. [65, Worthey 1994]; [63, Vazdekis
et al. 1996]; [4, Bressan et al. 1996];
[6, Bruzual & Charlot 1996)].
4000 Å break as a function of the main atmospheric stellar
parameters (namely effective temperature, surface gravity and
metallicity) in an ample stellar library which covers an appropriate
range of parameters to study relatively old stellar populations. One
of the main advantages of using fitting functions to describe the
behaviour of spectral indices is that they allow stellar population
models to include the contribution of all the required stars, through
a smooth interpolation in the space defined by the fitted stellar
parameters. The usefulness of this approach has been demonstrated by
the successful inclusion of similar fitting functions in recent
evolutionary synthesis models (e.g. [65, Worthey 1994]; [63, Vazdekis
et al. 1996]; [4, Bressan et al. 1996];
[6, Bruzual & Charlot 1996)].
It is important to keep in mind that the empirical calibration is only a mathematical representation of the break behaviour as a function of atmospheric stellar parameters, and that we do not attempt to obtain any physical justification of the derived coefficients.
We briefly review the previous works devoted to understand the D4000 in Sect. 2. The star sample is given in Sect. 3. The observations and data reduction are described in Sect. 4, whereas Sect. 5 contains a description of the error analysis. In Sect. 6 we show the behaviour of the measured D4000 values as a function of the stellar atmospheric parameters. The fitting strategy and the resulting empirical function are presented in Sects. 7. Finally, in Sect. 8 we give a summary, providing a public FORTRAN subroutine written by the authors to facilitate the computation of the D4000 using the fitting function presented in this paper. Sections 4 and 5 are rather technical, due to the inclusion of a lengthy explanation of the data and error handling. We suggest the reader not interested in such details to scan Tables 1 and 2, and skip those sections.
Copyright The European Southern Observatory (ESO)