3 Correlation statistics for basic variables

In our sample about 95% of the galaxies are of irregular and spiral type. Between their global parameters $V_{\rm m}$, $A_{25},\; L_{\rm B}, \; M_{\rm HI}$ rather close correlations can be seen, indicating important structural and dynamic properties of dwarf and giant galaxies. In Table 1 we present numerical parameters for the linear regression, $y = k\cdot x + c$, where the variables x and y correspond to logarithms of different integral characteristics of the galaxies. The table columns contain: N -- the number of galaxies in the subsample; r(x,y) -- the correlation coefficient in percent, its value from [11, Huchtmeier & Richter (1988)] is given in brackets; $\sigma(y)$ -- the standard deviation with respect to the regression line; k and c -- the regression parameters with their standard deviations.

Two upper lines in the table describe the Tully-Fisher relation for the galaxies with V₀ < 500 kms^-1. A comparison of r(x,y) values for our sample with the earlier data from HR shows good agreement. The scatter of galaxies on the Tully-Fisher diagrams appears to be lower when new photometric data and photometric distance estimates are used instead of kinematic ones, V₀/H. It should be noted that the linear diameter of a galaxy and its rotational velocity follow a linear relation with $k= 0.99\pm0.06$ in the whole range of diameters: from 1 Kpc to 40 Kpc. The same property was found also for thin disk-like galaxies viewed edge-on [14, (Karachentsev et al. 1999).] Apparently, the linear relation $A_{25}\propto V_{\rm m}$has a fundamental kinematic significance, reflecting conditions of formation and equilibrium of gaseous disks of galaxies.

Due to the tight correlations between luminosity, linear diameter and rotational velocity of the galaxies each of these parameters may be considered as a suitable argument to distinguish between giant, normal and dwarf objects. However, below we give preference to $V_{\rm m}$ as a variable which is independent of distance determination errors.

 

Figure 1: The relationship between the hydrogen mass-to-luminosity ratio and the rotational velocity. The solid line shows the least-squares regression. Some galaxies with extreme parameters, like NGC 205, DDO 154, UGCA 292, are indicated with their name in the figure. The quantities "r" and "k" in a corner correspond to the regression parameters in the Cols. (4) and (7) of Table 1

Figure 1 presents the distribution of the LV galaxies according to their rotational velocity and hydrogen mass-to-luminosity ratio. Here both variables are independent of the galaxy distance. These data confirm the well-known fact (HR, [20, McGaugh & de Blok 1997)] that the amount of hydrogen mass per unit of luminosity increases from giant spirals towards dwarfs. For some dwarf systems (K 90, DDO 154, and UGCA 292) their $M_{\rm HI}/L$ ratio reaches the maximum value, $\sim5 \;M_{\hbox{$\odot$}}/L_{\hbox{$\odot$}}$.The distribution of galaxies according to the "total" mass-to-luminosity ratio and rotational velocity is given in Fig. 2. Unlike $M_{\rm HI}/L,$ the M₂₅/L ratio tends to decrease from giant spirals to dwarf galaxies. The same result was derived by HR (line 14 in Table 1) and [3, Broeils & Rhee (1997).] It should be noted, however, that M₂₅/L is practically independent of the galaxy luminosity (line 6 in Table 1). Moreover, some authors (HR, [24, Salpeter & Hoffman 1996)] point even to a small increase in M₂₅/L towards dwarf galaxies, which gives grounds to assume a growth of relative amount of Dark Matter towards dwarf galaxies. But the origin of this difference may simply be caused by the statistical nature of the relations: $M_{25}/L\propto V_{\rm m}$and $M_{25}/L\propto L$, when mesurement errors of the observables have different influence on the correlation coefficients.

 

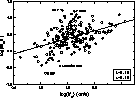Figure 2: The "total" mass-to-luminosity ratio versus the rotational velocity. The least-squares regression parameters, r and k, from Table 1 are shown in a corner

As it is seen in Fig. 2, the value of M₂₅/L for the considered galaxies occupies a range from 0.2 to $16 \;M_{\hbox{$\odot$}}/L_{\hbox{$\odot$}}$ with a median of $3.0 \;M_{\hbox{$\odot$}}/L_{\hbox{$\odot$}}$. The minimum "total" mass-to-luminosity ratios are characteristic of galaxies having a high surface brightness with signs of active star formation (NGC 1569, NGC 5253). The maximum M₂₅/L ratios are inherent in galaxies of low surface brightness like KK 210, PGC 18370, K 15 and K 90.

[26, Staveley-Smith & Davies (1988)] and [11, Huchtmeier & Richter (1988)] noted that the hydrogen mass-to-"total" mass ratio increases from giant towards dwarf systems. This known effect is also well seen in Fig. 3 for the sample of nearby galaxies.

 

Figure 3: The fractional HI mass shown as a function of rotational velocity. The solid line shows the least-squares regression. Some galaxies with extreme parameters, like NGC 205, DDO 154, UGCA 292, are indicated with their name in the figure. The quantities "r" and "k" in a corner correspond to the regression parameters in the Cols. (4) and (7) of Table 1

This relation has a clearer shape, when the rotational velocity is used as the argument instead of luminosity or linear diameter (see lines 7, 11, and 15 in Table 1). The median value of $M_{\rm HI}/M_{25}$ for the LV galaxies is about 0.25. Several dwarf systems like UGC 7949, K 215, and UGCA 292 have $M_{\rm HI}/M_{25}$ in the range of [1 - 3], which suggests that the true total mass of some dwarf galaxies exceeds their mass within R₂₅ at least by (2 - 3) times in accordance with [2, Broeils (1992).] An example of such a system is DDO 154 [4, (Carignan & Beaulieu, 1989).] But the three objects mentioned above seem to be even more HI-extended and unusual, deserving a detailed kinematic study in the HI line.

 

Figure 4: The HI surface density within the standard linear diameter (in M0 per Kpc2) as a function of rotational velocity. The solid line shows the least-squares regression. Some galaxies with extreme parameters, like NGC 205, are indicated with their name in the figure. The quantities "r" and "k" in a corner correspond to the regression parameters in the Cols. (4) and (7) of Table 1

In Fig. 4 a plot of the HI surface density (in $M_{\hbox{$\odot$}}$ per Kpc²) versus $V_{\rm m}$is displayed. The least-squares fit of these data, shown by the solid line, yields a slight decrease in $\Sigma_{\rm HI}$ towards giant galaxies unsignificant at the 1-sigma level.