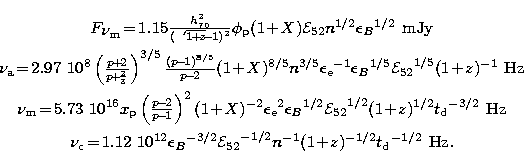Up: Physical parameters of GRB
We have derived the synchrotron frequencies and fluxes for a
relativistic blast wave expanding in a uniform medium. The results for
the peak flux, 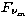 , the synchrotron self-absorption,
, the synchrotron self-absorption,
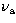 , peak,
, peak,  , and cooling,
, and cooling, 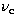 ,frequencies are summarised below (details can be found in
Wijers &
Galama 1999).
,frequencies are summarised below (details can be found in
Wijers &
Galama 1999).
| 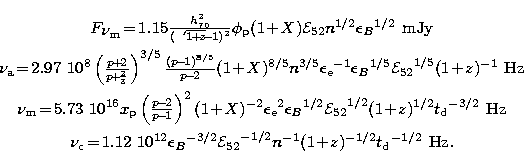 |
(1) |
| (2) |
| (3) |
| (4) |
Here 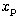 and
and 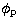 are the dimensionless spectral location and
dimensionless peak flux of a synchrotron spectrum from a power law
distribution of electron energies with index p. X is the hydrogen
mass fraction,
are the dimensionless spectral location and
dimensionless peak flux of a synchrotron spectrum from a power law
distribution of electron energies with index p. X is the hydrogen
mass fraction, 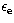 and
and 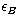 are the ratios of energy in
electrons and energy in the magnetic field to energy in nucleons,
respectively,
are the ratios of energy in
electrons and energy in the magnetic field to energy in nucleons,
respectively, 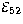 is the blast wave energy per unit solid
angle in units of 1052 erg, n is the nucleon density, h70=
H0/70 km s-1 Mpc-1, z the redshift and
is the blast wave energy per unit solid
angle in units of 1052 erg, n is the nucleon density, h70=
H0/70 km s-1 Mpc-1, z the redshift and 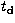 the
time in days since trigger
(see Wijers & Galama 1999).
We have
adopted an
the
time in days since trigger
(see Wijers & Galama 1999).
We have
adopted an 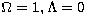 universe.
universe.


Up: Physical parameters of GRB
Copyright The European Southern Observatory (ESO)
![]() , the synchrotron self-absorption,
, the synchrotron self-absorption,
![]() , peak,
, peak, ![]() , and cooling,
, and cooling, ![]() ,frequencies are summarised below (details can be found in
Wijers &
Galama 1999).
,frequencies are summarised below (details can be found in
Wijers &
Galama 1999).