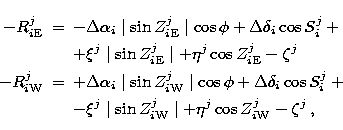
A global reduction method was applied for photoelectric astrolabe residuals. The approach is much simpler although more precise than the conventional method. The new form of the equations (Martin et al. 1996; Martin & Leister 1997) give us the possibility of using the entire set of the observing programme using the different data taken at two zenith distances.
In this method, the data and the unknowns are treated as symmetrically as possible with a determined statistical weighting. The used symmetric form aims to get the mean residuals with statistical independence and uniform variance.
Considering all the star observations (i) in the involved catalogues (j), we can write, for each transit (east and west - E and W), the following equations (Martin & Leister 1997):
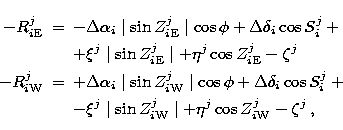 |
||
| (2) | ||
| (3) |
where:
![]() and
and ![]() are the east and west mean residuals
in zenith distance after the addition of group corrections for east
and west
transits of the star (homogenisation of the stellar groups), and
S is the parallactic angle. The constant
are the east and west mean residuals
in zenith distance after the addition of group corrections for east
and west
transits of the star (homogenisation of the stellar groups), and
S is the parallactic angle. The constant ![]() can be
understood as the difference between the
real and observed values of the latitude after the homogenisation
of the stellar groups (related with the equator correction);
the constant
can be
understood as the difference between the
real and observed values of the latitude after the homogenisation
of the stellar groups (related with the equator correction);
the constant ![]() is related to the true zenith distance of
observation (instrumental effects);
Z is the star azimuth from North to East;
is related to the true zenith distance of
observation (instrumental effects);
Z is the star azimuth from North to East; ![]() the local latitude,
and
the local latitude,
and ![]() the constant related to the equinox correction.
the constant related to the equinox correction.
Adding the mean residuals (![]() and
and ![]() ) above, the
stellar
declination corrections can be computed from astrolabe
observations by the
formula (Débarbat & Guinot 1970):
) above, the
stellar
declination corrections can be computed from astrolabe
observations by the
formula (Débarbat & Guinot 1970):
![\begin{eqnarray}
\nonumber
\Delta \delta_{i}& =& - [(R_{\rm E}+R_{\rm W})]_{i}^{...
...cos Z _{i}^{j}/\cos S_{i}^{j}+\\ & & + \zeta^{j}/\cos S_{i}^{j}\,,\end{eqnarray}](/articles/aas/full/1999/11/ds8172/img25.gif) |
||
| (4) |
From Eq. (3), we can write:
| (5) |
 |
||
| (6) |
where:
![]() =
= ![]() ; B1, B2, A1 are the magnitude
and colour index coefficients; mi is the visual apparent magnitude
of the star; Ii is the visual colour index (B-V) of the star
and
; B1, B2, A1 are the magnitude
and colour index coefficients; mi is the visual apparent magnitude
of the star; Ii is the visual colour index (B-V) of the star
and ![]() is the zenith distance correction.
is the zenith distance correction.
The possibility of computing absolute declinations rests on the
determination of ![]() .
.
This equation can be applied to all stars even to transit stars with
only one zenith distance to get systematic differences ![]() ,
which is not possible with the classical methods. For the stars which
are at maximum digression condition the coefficients of cosS
in the matrix vanishes, and these stars do not contribute to the
,
which is not possible with the classical methods. For the stars which
are at maximum digression condition the coefficients of cosS
in the matrix vanishes, and these stars do not contribute to the
![]() determinations.
determinations.
However, the system has a singularity, which is removed by the condition:
![]()
Copyright The European Southern Observatory (ESO)