One of the most important problems for the ground-based astronomy is
the limiting resolution of the image imposed by the atmospheric turbulence
in addition to the limit imposed by the optical instrument. The large
diameter of new telescopes increases the light collected by
the instrument but it cannot help to get a better spatial resolution
in the image. The atmospheric turbulence modifies in a stochastic way the
amplitude and the phase of the incoming wavefront and the images appear
degraded. Different parameters are used to characterize
the turbulence intensity in the atmosphere: Fried's parameter ![]() , the seeing
, the seeing ![]() , the
, the ![]() profiles,
the spatial coherence outer scale
profiles,
the spatial coherence outer scale ![]() , the isoplanatic angles
, the isoplanatic angles ![]() ,
the scintillation rate
,
the scintillation rate ![]() , the speckle boiling time
, the speckle boiling time
![]() and the wavefront coherence time
and the wavefront coherence time ![]() . Each of these parameters has a relevance for
particular astronomical applications. The outer scale
. Each of these parameters has a relevance for
particular astronomical applications. The outer scale ![]() , for
example, is fundamental for stellar interferometry and, in general, for
the large-ground-base interferometry as soon as the baseline is of the order or larger
than
, for
example, is fundamental for stellar interferometry and, in general, for
the large-ground-base interferometry as soon as the baseline is of the order or larger
than ![]() . It is known that the optical bandwidth
. It is known that the optical bandwidth ![]() is limited by the wavefront
coherence. If the base line L is less than
is limited by the wavefront
coherence. If the base line L is less than ![]() then
then
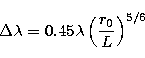 |
(1) |
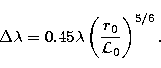 |
(2) |
The isoplanatic angle ![]() is a critical parameter for adaptive optics and
laser guide star technique.
We remember that, for example, the number of artificial stars necessary for a
complete sky covering is proportional to the inverse of the square of the
isoplanatic angle (Chester et al. 1990)
is a critical parameter for adaptive optics and
laser guide star technique.
We remember that, for example, the number of artificial stars necessary for a
complete sky covering is proportional to the inverse of the square of the
isoplanatic angle (Chester et al. 1990) ![]() .The coherence wavefront time
.The coherence wavefront time ![]() is particularly interesting because it gives
information about the so-called Greenwood frequency
is particularly interesting because it gives
information about the so-called Greenwood frequency ![]() which is often
used in specification of
adaptive optics control systems (Beckers 1993).
which is often
used in specification of
adaptive optics control systems (Beckers 1993).
At present, there are many reliable techniques (direct
and indirect) and instruments used to measure these parameters. We
recall the DIMM (Sarazin & Roddier 1981) for the seeing, the SCIDAR (Vernin & Azouit 1983a,b)
(optical measurements) and the instrumented
balloons (in situ measurements) for the ![]() profiles, the GSM
(Martin et al. 1994)
for the spatial coherence outer scale. These instruments are expensive,
need a lot of man-power, provide the relevant parameter for only one site and one line of sight
and have no predictive capability. In order to overcome these restrictions, following previous
attempts, we propose to use a
meteorological model coupled with a set of equations which links optical turbulence and
the air flow. In the past, some attempts have been made in
the study of seeing forecasting but none of the techniques previously tried could resolve
the issue by itself. The reasons of this failure is the
following. The seeing value is correlated to meteorological
parameters like the temperature, wind intensity and direction and to
geographic parameters like the orography. The problem is that the spatial
and temporal fluctuation scales of the seeing are much smaller than the
highest resolution attained by typical large scale (synoptic) meteorological forecasts.
We prefer, so, a medium-range scale model.
We give a brief summary of some of the interesting applications that this technique
could have in the astronomical context.
profiles, the GSM
(Martin et al. 1994)
for the spatial coherence outer scale. These instruments are expensive,
need a lot of man-power, provide the relevant parameter for only one site and one line of sight
and have no predictive capability. In order to overcome these restrictions, following previous
attempts, we propose to use a
meteorological model coupled with a set of equations which links optical turbulence and
the air flow. In the past, some attempts have been made in
the study of seeing forecasting but none of the techniques previously tried could resolve
the issue by itself. The reasons of this failure is the
following. The seeing value is correlated to meteorological
parameters like the temperature, wind intensity and direction and to
geographic parameters like the orography. The problem is that the spatial
and temporal fluctuation scales of the seeing are much smaller than the
highest resolution attained by typical large scale (synoptic) meteorological forecasts.
We prefer, so, a medium-range scale model.
We give a brief summary of some of the interesting applications that this technique
could have in the astronomical context.
Besides an accurate climatology, and a
nowcasting technic (Murtagh & Sarazin 1983),
such a numerical model could be a
useful tool for site testing. In spite of the recent excellent results obtained by
space telescopes, ground-based astronomy is today still competitive in many fields.
Finding the best place to install large modern
telescopes (![]() 8 m) is fundamental to attain the
maximum efficiency.
8 m) is fundamental to attain the
maximum efficiency.
Moreover, the scientific potential of the new generation telescopes is measured not only by the performance of the instruments placed at the focus of the telescope but by their proper use. The optimization of the "observing time programs'' (flexible scheduling) is mandatory to make a telescope competitive (Di Serego 1996; Di Serego 1997; Sarazin 1997; Masciadri et al. 1997). If very good seeing is predicted in the next few hours, optimized management of an observatory might decide to use high angular resolution instrument instead of a photometric one. However this is not an easy goal: seeing measurements obtained during the past campaigns (Munoz-Tuñón et al. 1997; Sarazin 1997; Racine 1996), show a short temporal stability (seeing characteristic time) of the order of 20-30 min. We intend to study whether an optimized numerical model could help in nightly programming the telescope observing time.
Finally, with a numerical technique we could obtain a global optical turbulence characterization. For a given time t0, 3-D maps (x, y, z) of all the parameters characterizing the optical turbulence in a region around the telescope could be forecast and we could estimate integrated values along different lines of sight. Hence, it is be better to talk about an "Optical Turbulence Forecast'' instead of a simple "Seeing Forecast''.
What is the state of the art of the seeing forecast for astronomical applications? We summarize, here, some of the most significant approaches provided by the literature.
Statistical technique
A statistical multiple regression (nearest-neighbor regression) was applied to
Paranal and La Silla sites (Murtagh 1993). This technique is not a
true prediction but rather a "nowcasting''. It tries to relate seeing
measurements to meteorological and environmental conditions at the same time
or in the near past.
Dynamical recurrent neural networks technique
The neural network is a non linear approach
to data series treatment. Its advantage, when compared to a statistical one, is that it
has a sort of inside memory that is the possibility to re-assimilate not only
the recent data but also the data of the past. Some authors (Aussem et al. 1994) tried
to apply it
to the astro-climatic forecasting but, to our opinion, they did not obtain particularly encouraging results.
Physical model technique
In the last decade, some authors (Coulman et al. 1988)
proposed a new approach based on the
measurements of the vertical gradient of the temperature. Assuming a universal behavior of the
outer scale of turbulence they deduced the vertical profile of the optical turbulence ![]() .
.
A different approach was tested by Van Zandt (Van Zandt et al. 1978, 1981). In the absence of any estimation of the geophysical outer scale L0, the authors developed a stochastic model based on a statistical treatment of the atmospheric vertical "fine structure''. This model was first used for astronomical purpose at the CFH telescope in Hawaii (Bely 1983) and it led to a poor correlation due to the impossibility of discriminating between boundary layer, dome and tracking seeing.
More recently, following the suggestions of a pioneering article (Coulman & Gillingham 1986)
which proposed of numerical modeling, the authors (Bougeault et al. 1995) implemented the hydrostatic numerical model
PERIDOT to forecast the seeing above a French site (Mt. Lachens). The model had
a 3 km ![]() 3 km resolution and it was supported by the French
radiosounding network, enabling good initialization of the
model. It gave satisfactory results but with some limitations:
3 km resolution and it was supported by the French
radiosounding network, enabling good initialization of the
model. It gave satisfactory results but with some limitations:
The model has not been applied yet to a high quality site. The best sites in the world have a mean seeing value of [0.5 - 1] arcsec with a very small fluctuation range of about [0.4 - 1.5] arcsec. Can numerical models forecast such low values? Can they forecast seeing with such a high precision as to discriminate between values in such a range?
In our opinion, the above mentioned limitations are due to the fact that the meteorological model was hydrostatic and thus it could make a significant error on the small scale component of the vertical velocity. It is true that in most cases, over flat terrain, one can assume a pure horizontal flow (hydrostatic hypothesis). Good observatories are generally installed on the top of high mountains and local effects are expected since the horizontal flux hits steep slopes. At observatory altitudes, ranging mainly between 2000 and 4000 meters, one can find strong winds that induce lee waves close to the summit and gravity waves can be encountered at higher altitudes, from say 5 to 15 km. It is known (Coulman et al. 1995; Tennekes & Lumley 1972; Tatarski 1961; Meteorological Monographs 1990) that optical turbulence is triggered by phenomena such as lee waves, gravity waves, jet stream or wind shear. Hence, it seems mandatory to us to discard the hydrostatic hypothesis and use the full non hydrostatic equations in the predicting model. Furthermore, many authors already noticed that most of the optical turbulence is concentrated in the boundary layer (the first kilometer) which is well taken into account by the use of both non-hydrostatic flow and fine horizontal grid size.
Copyright The European Southern Observatory (ESO)