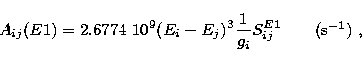Up: Atomic data from the
The calculations of transition probabilities
have been carried out with the computer
program SUPERSTRUCTURE, originally developed by Eissner
et al. (1974) and later modified by
Nussbaumer & Storey (1978) to ensure greater
flexibility in the radial functions. The method has been
described in previous IP reports (Galavís et al. 1997, 1998).
As discussed by Eissner (1991)
the LS terms are represented by CI wavefunctions of the type
| 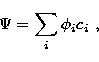 |
(2) |
where the configuration basis functions 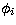 are constructed from
one-electron orbitals generated in two types of potentials
are constructed from
one-electron orbitals generated in two types of potentials 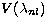 :the spectroscopic orbitals P(nl) are calculated in a
statistical Thomas-Fermi-Dirac model potential
(Eissner & Nussbaumer 1969) whereas the correlation
orbitals
:the spectroscopic orbitals P(nl) are calculated in a
statistical Thomas-Fermi-Dirac model potential
(Eissner & Nussbaumer 1969) whereas the correlation
orbitals  are obtained in a Coulomb potential
(Nussbaumer & Storey 1978). With regards to
configuration bases, four approximations are considered as shown in
Table 1. Approximation A is our main standard framework containing only
configurations with
are obtained in a Coulomb potential
(Nussbaumer & Storey 1978). With regards to
configuration bases, four approximations are considered as shown in
Table 1. Approximation A is our main standard framework containing only
configurations with  orbitals. The representations for the
lower members of the sequence are progressively refined with
approximations B, C and D which include configurations with
n=4 orbitals of increasing complexity.
The adopted variational procedure minimises
with equal weights the sum of energies of all the terms in specific
configurations, that is
orbitals. The representations for the
lower members of the sequence are progressively refined with
approximations B, C and D which include configurations with
n=4 orbitals of increasing complexity.
The adopted variational procedure minimises
with equal weights the sum of energies of all the terms in specific
configurations, that is
| 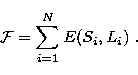 |
(3) |
The 1s, 2s and 2p orbitals are chosen to minimise the sum of energies of the
three terms in the 2s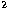 2p
2p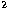 ground configuration. The
ground configuration. The  s,
s,
 p and
p and  d correlation orbitals are subsequently chosen to
minimise the sum of the energies of the twelve terms of the n=2 complex.
Finally, the
d correlation orbitals are subsequently chosen to
minimise the sum of the energies of the twelve terms of the n=2 complex.
Finally, the 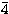 s,
s, 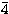 p,
p, 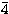 d and
d and 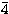 f correlation
orbitals in approximations B, C and D are optimised on the sum of the
energies of the three terms within the ground configuration. The final
scaling parameters are listed in Table 2.
f correlation
orbitals in approximations B, C and D are optimised on the sum of the
energies of the three terms within the ground configuration. The final
scaling parameters are listed in Table 2.
Table 1:
Configuration bases used in approximations A, B, C and D
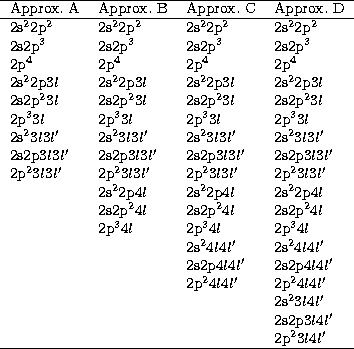 |
Table 2:
Scaling parameters 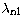 used to generate the orbitals
for the four approximations (A, B, C and D) as a function of nuclear charge
number Z. The negative scaling parameters denote Coulombic correlation
orbitals
used to generate the orbitals
for the four approximations (A, B, C and D) as a function of nuclear charge
number Z. The negative scaling parameters denote Coulombic correlation
orbitals
 |
In SUPERSTRUCTURE the Hamiltonian is taken to be of the form
|  |
(4) |
where 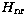 is the usual non-relativistic Hamiltonian. The
relativistic corrections
is the usual non-relativistic Hamiltonian. The
relativistic corrections 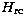 are taken into account through the
Breit-Pauli (BP) approximation (Jones 1970, 1971)
are taken into account through the
Breit-Pauli (BP) approximation (Jones 1970, 1971)
| ![\begin{eqnarray}
H_{\rm rc}= & \sum_{i=1}\sp N [f_i({\rm mass})+f_i({\rm d})+f_i...
... \\ & \sum_{i\gt j}[g_{ij}({\rm so}+{\rm so}')+g_{ij}({\rm ss}')]\end{eqnarray}](/articles/aas/full/1999/04/ds1589/img36.gif) |
|
| (5) |
where the one-body terms 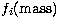 ,
, 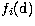 and
and 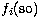 correspond respectively to the mass-variation correction, the Darwin term and the
spin-orbit interaction; the two-body Breit terms
correspond respectively to the mass-variation correction, the Darwin term and the
spin-orbit interaction; the two-body Breit terms  and
and 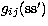 are the spin-other-orbit plus mutual spin-orbit and
spin-spin interactions. In the present calculations, the spin-spin interaction,
when included, is fully taken into account for the first three configurations
in Table 1, i.e. the spectroscopic configurations. To estimate the spin-spin
contribution for all configurations in the largest basis set considered here
would be very costly, if not impossible. Fortunately, small-scale tests showed
that the numbers reported here are not affected by more than a few % at low
Z by this approximation. When Z increases, this effect decreases rapidly.
Two-body non fine-structure terms are currently neglected in
SUPERSTRUCTURE.
are the spin-other-orbit plus mutual spin-orbit and
spin-spin interactions. In the present calculations, the spin-spin interaction,
when included, is fully taken into account for the first three configurations
in Table 1, i.e. the spectroscopic configurations. To estimate the spin-spin
contribution for all configurations in the largest basis set considered here
would be very costly, if not impossible. Fortunately, small-scale tests showed
that the numbers reported here are not affected by more than a few % at low
Z by this approximation. When Z increases, this effect decreases rapidly.
Two-body non fine-structure terms are currently neglected in
SUPERSTRUCTURE.
From perturbation theory, the relativistic wavefunction  can
be expanded in terms of the non-relativistic functions
can
be expanded in terms of the non-relativistic functions  :
:
|  |
(6) |
This expansion demonstrates the importance of accurate term energy separations
when constructing the relativistic wave functions  .Using accurate experimental level energies (Edlén 1985),
.Using accurate experimental level energies (Edlén 1985),
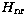 is adjusted in order to obtain term energies (calculated from the
weighted fine-structure level energies) which match experiment.
This semi-empirical term energy correction (TEC) procedure was
originally implemented in SUPERSTRUCTURE by Zeippen et al.
(1977). Galavís et al. (1997, 1998) have shown that, in the treatment of
the forbidden transitions in the carbon and oxygen sequences and of the
intercombination transitions in the boron sequence, the inclusion of TECs
can lead to a high degree of accuracy with a much reduced configuration basis
than in a comparable purely ab initio treatment.
This previous experience led to the choice of our standard representation
(approximation A). Of course,
the validity of this semi-empirical procedure must be checked in
the case under consideration here.
is adjusted in order to obtain term energies (calculated from the
weighted fine-structure level energies) which match experiment.
This semi-empirical term energy correction (TEC) procedure was
originally implemented in SUPERSTRUCTURE by Zeippen et al.
(1977). Galavís et al. (1997, 1998) have shown that, in the treatment of
the forbidden transitions in the carbon and oxygen sequences and of the
intercombination transitions in the boron sequence, the inclusion of TECs
can lead to a high degree of accuracy with a much reduced configuration basis
than in a comparable purely ab initio treatment.
This previous experience led to the choice of our standard representation
(approximation A). Of course,
the validity of this semi-empirical procedure must be checked in
the case under consideration here.
The radiative rate for an electric dipole (E1) transition is given by the
expression
| 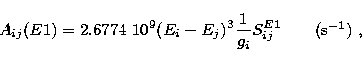 |
(7) |
where gi is the statistical weight of the upper initial level i and
energies E are expressed in Rydbergs. It is clear
that the accuracy of the calculated A-values depends primarily
on the quality of the wavefunctions used in evaluating the line
strengths SijE1, but even relatively small errors in the energy
differences (Ei-Ej) can reduce it because of the exponent 3 in (7).
Therefore,
the transition probabilities are computed with
an accurate and consistent dataset of experimental energy levels
(Edlén 1985).


Up: Atomic data from the
Copyright The European Southern Observatory (ESO)
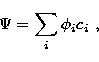
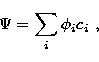

![\begin{eqnarray}
H_{\rm rc}= & \sum_{i=1}\sp N [f_i({\rm mass})+f_i({\rm d})+f_i...
... \\ & \sum_{i\gt j}[g_{ij}({\rm so}+{\rm so}')+g_{ij}({\rm ss}')]\end{eqnarray}](/articles/aas/full/1999/04/ds1589/img36.gif)
![]() can
be expanded in terms of the non-relativistic functions
can
be expanded in terms of the non-relativistic functions ![]() :
: