4 Discussion

Several important trends have been identified as a result of the analysis of cloud rotational data in Sect. 3. It seems clear, in the first place, that angular velocity vectors in isolated clouds and complexes show a preferential orientation with respect to the galactic plane; a feature which would support an origin for cloud angular momenta in galactic rotation. This trend is not however shared by clumps and condensations within the clouds. Secondly, it appears that cloud rotation may be important for the stability of a surprisingly large number of these clouds, and influence observed aspect ratios. Thirdly, it appears that the trends for angular velocity and specific angular momentum are inconsistent with angular momentum conservation, turbulent vorticity, and models of axisymmetric, isothermal, non-magnetic clouds. Finally, it appears that angular momentum vectors for rings and (principally) disks possess a tendency towards non-random orientation, whilst rotational stabilisation is likely also to be important; characteristics which are to be found in neither clumps nor condensations. It is also notable that trends in J/M, J and $\Omega$ with cloud radius R differ from those of other sub-groups in this study.

It would appear, in brief, that disks are generically different from most other clouds investigated here; a feature which may argue for a physically distinct evolutionary sequence and, in all probability, reflects their differing spatio-kinematic structures. It is apparent, for instance, that these sources not only display typically large aspect ratios $\Gamma$ (although intrinsic values of this parameter are likely to be even greater), but also that angular velocities are among the most extreme, and the proportionate mass of embedded stars $M_{\rm ast}/M$ is substantial (viz. Table 1). As a result, and more than for any other cloud subgroup, disk momentum depends upon the proportion of angular momentum carried by the stellar mass fraction, and the degree of angular momentum transfer that has occurred during protostellar contraction and subsequent evolution.

Although we have previously noted that turbulent vorticity gradients appear too large to explain observed overall trends in $\Omega(R)$, this is less the case for certain cloud subgroups. In particular, the variation in dln$\Omega$/dlnR = -0.67 predicted by Fleck & Clark (1981) is not too different from that estimated for clouds ($\cong - 0.53$) and condensations ($\cong -0.60$) taken separately.

The theory of Fleck and Clark requires however to be somewhat revised. In particular, these authors assume strict energy cascade from large to small turbulent eddy scales, whence turbulent velocity $V_{\rm turb}\propto R^{0.33}$. In reality, however, it seems that most of the clouds in this study are likely to be characterised by supersonic turbulence (e.g. Myers 1983), and compressible fluid interactions, whence $V _{\rm turb}$ (R) may depart considerably from the trend predicted by Kolmogoroff theory (Fleck 1983).

If, in place of this, one therefore employs the observed relation $V_{\rm turb}\propto R^{0.5}$ (see for instance Myers (1983), and also the recent commentary by Phillips 1998), it is then possible to evaluate a revised vorticity gradient dln$\Omega$/dlnR = -0.5.

Although this latter parameter is somewhat greater than supposed before, it would still (within uncertainties) be consistent with the relations noted for clouds and condensations. In the case of condensations alone, therefore, it may be possible to comprehend observed variations in rotational parameters in terms of turbulent interactions. Such an explanation is likely to be less relevant in the case of isolated clouds and complexes, however, given the orientational disposition of their vectors $\Omega$.

It may also, on the other hand, be possible to explain certain of the functional trends in rotation in terms of magnetic braking. Thus, where cloud fields are appreciably greater than in the intercloud medium, and the density contrast between cloud and exterior medium is given by $\rho_{\rm c}/\rho_{\rm m}$, angular momentum would be transferred outwards over a time-scale (Gillis et al. 1974, 1979; Mestel & Paris 1979, 1984)

$$\tau_\omega\cong0.27\left[\frac{M^2Ga}{B^2R^4b}\right]^{0.5}\left[\frac{ \rho_{\rm c}}{\rho_{\rm m}}\right]^{0.1}\tau_{\rm ff}$$ (6)

where the free-fall timescale

$$\tau_{\rm ff}=\left[\frac{3\pi}{32G\rho_{\rm c}}\right]^{0.5}$$ (7)

and parameter b=0.75 for a sphere and $\pi^{-1}$ for a disk. The value of a is given by ($1 - \gamma/3)/(1 - 2\gamma/5)$ for a radial cloud density variation $\rho(r) \propto r^{-\gamma}$; we shall simply assume here a value a = 1, appropriate for spheres with uniform density. Substituting $\rho_{\rm c}/\rho_{\rm m}\sim 10$, and $B \cong 12 ~\mu$G (Phillips 1998) then yields $\tau_\omega\cong 2.45\ 10^4$ $(M/M_\odot)^{0.5}$ (R/pc)^-0.5 yrs $\cong$ 3.8 10⁵ (R/pc)^0.23 yrs.

How does this compare with observations? The first characteristic to note is that the gradient dln(J/M)/d$M \cong 0.7$ is actually less than would be predicted for isothermal models of non-magnetic rotating clouds. If one assumes, on the other hand, that the logarithmic decrement in J/M arises primarily from magnetic braking, and that there is an evolutionary trend from large to small cloud structures, then a fractional reduction in specific angular momentum $1 - f = \delta(J/M)/(J/M) = 0.7$ would imply comparatively large radial changes $\Delta R/R = (1 - f^{0.79}) \cong 0.6$. It is apparent, in brief, that the decrement in J/M is not only uniform and continuous in R and M, but appears also to be comparatively shallow; we perceive no evidence for the strong magnetic braking which has been presumed heretofore.

Several routes might be suggested whereby this problem could be side-stepped. Thus, it is possible to assume that values B have been greatly overestimated; a presumption which seems unlikely given the observations of this parameter through Zeeman splitting (cf. Myers & Goodman 1988). An alternative possibility is that a large fraction of clouds are magnetically supercritical, and possess density contrasts $\rho_{\rm c}/\rho_{\rm m} \gt 10$, leading to reduced values of $\tau_\omega$ (McKee et al. 1993); a situation which may be particularly applicable to GMC's (McKee 1989).

Finally, we note that cloud contraction velocities $V_{\rm c}\geq V_\nu$ (where $V_\nu$ is the Alfven velocity) would lead to the trapping of Alfven waves (Mouschovias 1989), and a considerable reduction in the rate of angular momentum transfer. In particular, given that

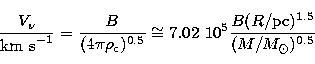$$\frac{V_\nu}{{\rm km\ s}^{-1}}=\frac{B}{(4\pi\rho_{\rm c})^{... ...\cong 7.02\ 10^5 \frac{B(R/{\rm pc})^{1.5}}{(M/M_\odot )^{0.5}}$$ (8)

then for $B \sim 12 ~\mu$G we obtain $V_\nu = 0.55$ (R/pc)^0.78 km s^-1 (where we have also substituted for M(R) from Table 2). Given also that free-fall collapse velocities $V_{\rm ff} = (2GM/R)^{0.5}\cong 1.42(R/{\rm pc})^{0.23}$ km s^-1, then $V_{\rm ff} \geq V_\nu$ for $R\leq 1.7$ pc. Trapping may therefore be possible over comparatively short periods, where contraction occurs at velocities comparable or greater than the free fall velocity $V_{\rm ff}$ - a situation which may, in turn, arise through external cloud compression by winds and expanding shells (e.g. Elmegreen & Lada 1977; although note that radial decrements in $V_\nu$ are likely to be less steep given a dependency $B \propto \rho_\alpha$, $1/3 \leq \alpha\leq 1/2$ (Gordon 1988)). The mean velocity of contraction for clouds taken as a whole, on the other hand, is on the order of $<V_{\rm c}\gt = R_0m_{\rm ast}/\varepsilon M_{\rm cx} \cong\allowbreak 0.34$ km s^-1, where $m_{\rm ast}\cong 3\ M_\odot$ yr^-1 is the mean galactic rate of star formation, $\varepsilon \cong 0.1$ is the efficiency of star formation (Vrba 1977), and $M_{\rm cx}\cong 4\ 10^9\ M_\odot$ is the mass of gas in the form of molecular complexes (Solomon & Sanders 1980). The parameter $<V_{\rm c}\gt$ (which may be regarded as lower limit velocity for quiescent and continuous contraction) is therefore only a little less than $V_\nu$ for moderately sized clouds.

It is therefore conceivable that a trapping mechanism of kind noted above may indeed operate to reduce rates of angular momentum transfer; although the effectiveness of this process is undoubtedly enhanced where contraction proceeds in fits and starts, rather than through a uniform global decrease in radius.

Finally, we have failed in the above discussion to address several outstanding questions, including the unusually close correlation between angular momentum J and non-virial cloud mass M (Fig. 6), and the strange disparity in rotational properties between disks, and both clumps/condensations and larger cloud structures. In this latter respect, we note that one conceivable solution to the (possible) orientational disparity between clumps/condensations and disks may be that clumps, after all, are not rotating; that despite the attribution of rotation to these features in the literature, we are in fact (say) witnessing the superposition of differing, unrelated features. A problem with this supposition, however, is that the broad trends in $\Omega$, J, and J/M noted for clumps and condensations are also closely similar to those determined for clouds - and not too far removed from those for disks as well (although to be sure, disks are in this respect somewhat different from all other subgroups). Such a correspondence would not be anticipated were gradients to arise from random clump superposition.

This can be expressed in a slightly more precise way. Thus, if we assume that projected clump radii $\Delta R$ are, in the mean, invariant with cloud size, and that the mean separation between unresolved clump-pairs is also constant (consistent with the approximate invariance in cloud column densities), then the typical angular velocity attributed to such superpositions would be $\Omega\propto \sigma_{\rm turb}/\Delta R \propto\sigma_{\rm turb}$ (where $\sigma_{\rm turb}$ is the line of sight velocity dispersion due to turbulence). If we assume virial stability, and employ a relation dln$M_{\rm vir}$/dlnM = 0.73 based on a least squares analysis of the present results (thermal velocity contributions to line width can normally be regarded as small, and have been ignored (viz. Myers 1983)), then cloud mass $M \propto\sigma_{\rm turb}^{2.56}$. As a consequence, one would then anticipate $\Omega\propto M^{0.37}$, and (given $M \propto R^{0.78}$ from Table 2) $J \propto M^{3.9}$. These relations are not consistent with the trends noted in Sect. 3.

On the other hand, it is by no means unreasonable that clump orientations should be so disordered; supersonic and magnetic interactions are sufficient to ensure appreciable orientational randomisation of the angular velocity vectors $\Omega$. The real mystery, in all probability, is why fossil echoes of prior orientations should be retained by disk-like structures alone.