We employ the Breit-Pauli R-matrix method (Scott & Burke 1980) to calculate
the photoionization cross sections. This method has the advantage of including
the effects of resonances which converge onto the LSJ target states of Fe XIX
which are included in the calculation. The present work is based on including
in the eigenfunction expansion the following 11 Fe XIX LS target states,
![]() : 2s22p4 3P, 2s22p4 1D, 2s22p4 1S,
2s2p5 3P
: 2s22p4 3P, 2s22p4 1D, 2s22p4 1S,
2s2p5 3P![]() , 2s2p5 1P
, 2s2p5 1P![]() , 2p6 1S,
2s22p33s 3S
, 2p6 1S,
2s22p33s 3S![]() , 2s22p33s 3P
, 2s22p33s 3P![]() , 2s22p33s
3D
, 2s22p33s
3D![]() , 2s22p33s 1D
, 2s22p33s 1D![]() and 2s22p33s
1P
and 2s22p33s
1P![]() . Each of these target states are represented by configuration
interaction wavefunctions of the form
. Each of these target states are represented by configuration
interaction wavefunctions of the form
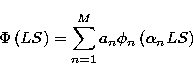 |
(1) |
![\begin{displaymath}
P_{nl}\left(r\right) =
\sum_{j=1}^{k}c_{jnl}\left[
\frac{\le...
...right)! } \right]^{\frac12}
r^{I_{jnl}}{\rm e}^{-\zeta_{jnl}r}.\end{displaymath}](/articles/aas/full/1998/20/h0926/img7.gif) |
(2) |
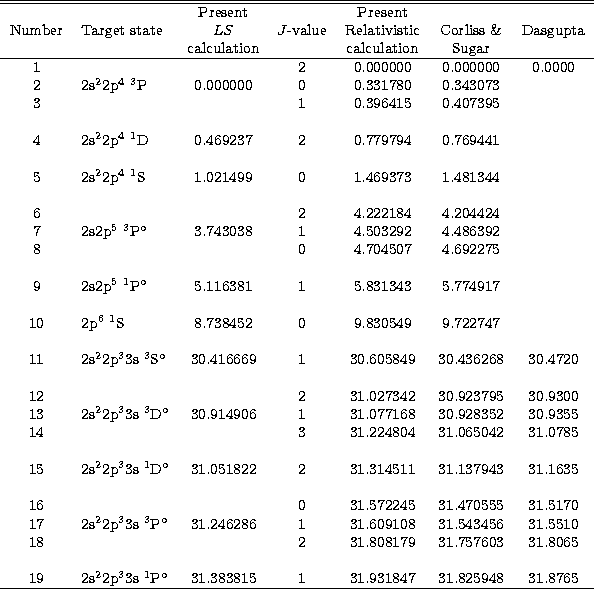
The energies obtained for these target states were calculated in LS-coupling
using the CIV3 configuration interaction code and in LSJ-coupling using the
RECUPD module of the R-matrix codes where the same orbitals and level of
correlation were used in each case. The results of both calculations are
presented in Table 2
and compared with the experimental results tabulated
by Corliss & Sugar (1982)
and the relativistic calculations of Dasgupta
(1995)
(using the non-relativistic operators plus the spin-orbit operator,
mass correction operator and the Darwin term). (Note that a comparison between the
LS calculation and the data of Corliss & Sugar requires consideration of a
weighted average of the ground state provided by Corliss & Sugar). Clearly
some discrepancy exists between the LS-coupling calculation and the previous
studies. However, attempts at introducing further correlation into this
calculation had minimal effects on these energies. Threshold positions and
thus resonance positions in general would have been of insufficient accuracy if
a solely LS-coupling calculation had been performed. Thus, it is clearly essential
to include relativistic effects, in that the introduction of interaction
between different ![]() symmetries is highly relevant to the accuracy of the
target state energies. The results of the LSJ-coupling calculation are
highly satisfactory and examination of the eigenvectors verifies that
significant mixing between different
symmetries is highly relevant to the accuracy of the
target state energies. The results of the LSJ-coupling calculation are
highly satisfactory and examination of the eigenvectors verifies that
significant mixing between different ![]() symmetries possessing the same
symmetries possessing the same
![]() value does indeed occur particularly in the ground state terms. (For
example in the LS calculation the ground state, 3P, is reasonably pure
but in the relativistic calculation 11% of the 3P2 ground state is
made up of the 2s22p4 1D2 configuration. This is enough to lower
the ground state by as much as 8 a.u.).
value does indeed occur particularly in the ground state terms. (For
example in the LS calculation the ground state, 3P, is reasonably pure
but in the relativistic calculation 11% of the 3P2 ground state is
made up of the 2s22p4 1D2 configuration. This is enough to lower
the ground state by as much as 8 a.u.).
 |
The (N+1)-electron wavefunction, ![]() is expanded in the following manner
is expanded in the following manner
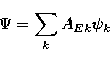 |
(3) |
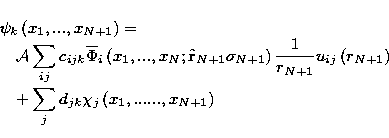 |
(4) |
Using an R-matrix radius of 2.2 a.u., 25 continuum orbitals for each value of ![]() and a free electron energy mesh of
and a free electron energy mesh of ![]() Ryd, the R-matrix
codes (Berrington et al. 1987; Seaton 1987)
are then utilized
to calculate the photoionization
cross sections. The ionization energy of the Fe XVIII
ground state was found to be 99.954 Ryd, in excellent agreement with the experimental
value of
Ryd, the R-matrix
codes (Berrington et al. 1987; Seaton 1987)
are then utilized
to calculate the photoionization
cross sections. The ionization energy of the Fe XVIII
ground state was found to be 99.954 Ryd, in excellent agreement with the experimental
value of ![]() Ryd tabulated by Corliss & Sugar (1982).
The
2s22p5 2P
Ryd tabulated by Corliss & Sugar (1982).
The
2s22p5 2P![]() Fe XVIII bound state was found to be at
0.96068 Ryd relative to the ground state, compared with the value 0.93541
Ryd given by Corliss & Sugar (a difference of only 2.6%), suggesting that
the approach used in the calculation of bound states is of sufficient
accuracy.
Fe XVIII bound state was found to be at
0.96068 Ryd relative to the ground state, compared with the value 0.93541
Ryd given by Corliss & Sugar (a difference of only 2.6%), suggesting that
the approach used in the calculation of bound states is of sufficient
accuracy.
Copyright The European Southern Observatory (ESO)