3 Roche model and procedure of light curve analysis

In the present paper, the WZ Cep photoelectric observations were analysed to study the activity of the system. For analysing these asymmetric light curves, probably deformed by the presence of spotted areas on the components, we used the programme of Djurasevic (1992a), which is based on the Roche model and the principles originated in the paper by Wilson & Devinney (1971). The light curve analysis was made by applying the inverse problem method (Djurasevic 1992b) based on Marquardt's (1963) algorithm.

According to this method, the stellar size in the model is described by the filling coefficients for the critical Roche lobes F_1,2 of the primary and secondary component, respectively, which indicate to what degree the stars of the system fill their corresponding critical lobes. For synchronous rotation of the components these coefficients are expressed via the ratio of the stellar polar radii, R_1,2, and the corresponding polar radii of the critical Roche lobes, i.e., $F_{1,2}=R_{1,2}/R_{\rm Roche_{1,2}}$. The model is generalised to the case of an overcontact configuration, which is characteristic for the W UMa-type systems. In this case the potential $\Omega_{1,2}$ characterising the common photosphere is derived with the filling coefficient of the critical Roche lobe F₁>1 of the primary, while the coefficient F₂ may be excluded from further consideration. The degree of overcontact, is defined in the classical way (Lucy & Wilson 1979) as:

$$f_{\rm over}[\%]=100\cdot(\Omega_{1,2}- \Omega_i)/(\Omega_0-\Omega_i),$$

where $\Omega_{1,2}$, $\Omega_i$, and $\Omega_0$ are the potentials of the common photosphere and of the inner and outer contact surfaces, respectively. Since the potentials $\Omega_i$ and $\Omega_0$ include Lagrangean equilibrium points L₁ and L₂ respectively, they can be easily derived. Namely, in the mentioned points the net force acting in the system is equal to zero.

In a spherical coordinate system the surfaces of the components are divided into a large number of elementary cells, whose intensity and angular distribution of radiation are determined by the stellar effective temperature, limb-darkening, gravity-darkening and by the effect of reflection in the system. The presence of spotted areas (dark or bright) enables one to explain the asymmetries, the light curve anomalies and the O'Connell effect on the light curves of active CBs. In our programme these active regions are approximated by circular spots, characterised by the temperature contrast of the spot with respect to the surrounding photosphere ($A_{\rm s}=T_{\rm s}/T_{*}$), by the angular dimension (radius) of the spot ($\theta$) and by the longitude ($\lambda$) and latitude ($\varphi$) of the spot centre. The longitude ($\lambda$) is measured clockwise (as viewed from the direction of the +Z-axis) from the +X-axis (line connecting star centres) in the range $0^{\rm o} - 360^{\rm o}$. The latitude ($\varphi$) is measured from $0^{\rm o}$ at the stellar equator (orbital plane) to $+90^{\rm o}$ towards the "north" (+Z) and $-90^{\rm o}$ towards the "south" (-Z) pole. The generalisation of the computer model (Djurasevic 1992a) to the case of an overcontact configuration reveals the high importance of the "visibility" of elementary cells around the neck region. In order that, at a chosen orbital phase, the radiation from elementary cells, in which the stellar surface is divided, reaches the observer, a classical procedure is to check the fulfilling of the condition: $\cos \gamma\gt 0;$ no eclipsing by other system's component. Here, $\gamma$ is the angle between the unit vector directed toward the observer, ${\vec a}_0$, and the vector ${\vec n}$ perpendicular to the elementary cell. For elementary cells around the neck region between stars in an overcontact configuration the mentioned criterion is necessary but not a sufficient one for calculating of the radiation fluxes reaching the observer. Namely, the curvature's sign of the equipotential surface, characterising the common photosphere (the ridge saddle region), changes around the neck region. Therefore, in this region the "visibility" condition $\cos \gamma \gt 0$ is not sufficient for certain number of elementary cells. At some orbital phases these elementary cells can be hidden by the body of the component star they belong to, and this fact needs extra checking. The very effective checking procedure is based on ideas and principles exposed in one of mentioned Djurasevic's papers (1992a), so we won't go into details here. In principle, the problem is solved by calculating the potential $\Omega(x,y,z)$ along the line crossing the centre of the elementary cell towards the observer, and by comparing this potential to the potential of the overcontact configuration $\Omega_{1,2}$. If $\Omega(x,y,z) \gt \Omega_{1,2}$ is fulfilled the elementary cell is hidden by the stellar body.

We emphasize this problem, because our checking procedure of the "visibility" of elementary cells is different from that applied in the WD code. To achieve more reliable estimates of the model parameters in the programme for analysing the light curves, we applied a quite dense coordinate grid having $72\times144=10368$ elementary cells per each star.

For a successful application of the foregoing described model in analysing the observed light curves, the method proposed by Djurasevic (1992b) was used. The interpretation of photometric observations is based on the choice of optimum model parameters yielding the best agreement between the observed light curve and the corresponding synthetic one. Some of these parameters can be determined a priori in an independent way, while the others are found by solving the inverse problem. We obtained optimum model parameters through the minimisation of $S=\Sigma(\rm O-C)^2$, where O-C is the residual between observed (LCO) and synthetic (LCC) light curves for a given orbital phase. The minimisation of S is done in an iterative cycle of corrections of the model parameters. In this way the inverse problem method, based on Marquardt's algorithm, allows us to estimate the system's parameters and find the standard errors.

An earlier estimate of the spectral type (F2) given in GCVS (Kukarkin et al. 1969), made a slight confusion in choosing of the values for the gravity-darkening coefficients of the component stars, $\beta_{1,2}$. This spectral type is in the transition domain between stars possessing convective and radiative envelopes. It appears that the value of the gravity-darkening coefficients greatly affects the fitting quality. If we take them as free parameters in the inverse problem, the increase of the $\beta_{1,2}$ coefficients' value beyond 0.08 reflects its self in the shape of light curve similarly to the effect of the increase of the overcontact $(f_{\rm over}[\%])$. This involves further problems in the interpretation of the light curve. The gravity-darkening exponents $\beta_{1,2}$, following Lucy (1967) and Rafert & Twigg (1980), were set to 0.25 or 0.08 according to the temperature, with the switch at 7200 K. The higher value corresponds to von Zeipel's law for a fully radiative envelope. The reflection coefficients (albedos) were set to 1.0 or 0.5, corresponding to full or partial reradiation, with the same switch criterion. According to newGCVS (Kholopov et al. 1985) the spectral type of WZ Cep is estimated as F5, so the system's components possess convective envelopes. Based on this spectral type and using Basic Stellar Data of Lang (1991), the temperature of the primary was fixed at T₁=6440 K. According to the mentioned criterion, we adopted the values of 0.08 and 0.5 for the coefficients $\beta_{1,2}$ and the albedos A_1,2 respectively.

In solving the inverse problem, the values of the limb-darkening coefficients were derived from the stellar effective temperature and surface gravity, according to the given spectral type, by using the polynomial proposed by Díaz-Cordovés et al. (1995). During the optimisation process, according to the temperature changes we have an automatic recomputation of the limb-darkening. For the R filter the limb-darkening is taken from the tables published by Al Naimy (1977). The present analysis yields F₁>1 for the filling coefficient in the critical Roche lobe, i.e. to an overcontact configuration. So, we expect mutual tidal effects of the components to cause synchronisation between the stellar rotational period and the system's orbital period. Therefore, in solving the inverse problem we adopted $f_{1,2}=\omega{1,~2}/\omega_{\rm K}=1.0$ for nonsynchronous rotation coefficients, where f_1,2 is the ratio of the components' angular rotation rate ($\omega_{1,2}$) to the Keplerian ($\omega_{\rm K}$) orbital revolution rate. The light-curve analysis show that the more-massive (primary) component is eclipsed at the primary minimum. Moreover, since the results of the light curve analysis strongly depend on the choice of the adopted working hypothesis, the present analysis was carried out within the framework of several hypotheses (bright and dark spotted areas on the primary or on the secondary).

In analysing the light curves the following procedure is applied. Based on its quite symmetric shape, we analyse first our new B, V, R light curves, as relatively free of spot effects. In their analysis we avoided the somewhat questionable practice of forming normal points, and included all observations. The optimisation begins using only the basic model parameters. In the inverse problem solution we started from the configuration in which the components do not fill their Roche lobes. The iterating process of optimisation converges very fast to the overcontact configuration with the mass-ratio of the components about 0.33, almost equal temperatures of the components and with orbit inclination about $85^{\rm o}$. After achieving the first convergence, one also includes free parameters related to spots into the iterative optimisation process. Best fitting of the observations is achieved under the assumption of a single spotted area on the primary star. If we treat the spots' temperature contrast as free parameters in the inverse problem, the light-curve analysis gives the values of about $A_{\rm s}=T_{\rm s}/T_1\sim0.7$. So, in the final phase of our computations we adopt this value, which reduces the number of free parameters and provide more reliable estimates of other model elements. According to our analysis, the relatively small spotted area is located near the neck region between components.

Obtained in this way basic parameters of the system are used as starting points in the inverse problem for very asymmetric Hoffmann's light curves. Namely, the experience proves that the estimation of spots' parameters can be on the account of the quality of the estimation of system's basic parameters. If the optimisation starts simultaneously with all free parameters, Hoffmann's light curves could give also the solution with satisfying fit of the observation without the overcontact configuration. Therefore, it is very important that system's basic parameters are estimated via the less deformed light curves. In this case the optimisation starts with the spot's parameters. When the optimisation based on these parameters does not provide a further minimisation of $\Sigma(\rm O-C)^2$, the system's basic parameters have to be introduced in the iterative process. Namely, one cannot in advance exclude the possibility that some of these parameters can change during the analysed period of time. Using this procedure we optimise all free-parameters of the model in the final iterations.

The analysis of Hoffmann's (1984) observations is based on normal points (Kaluzny 1986), translated into the scale of magnitudes and normalised to the brightness at the orbital phase of 0.25. The large degree of asymmetry in these light curves Kaluzny (1986) explained by assuming a "hot spot" on one side of the system. In the frame of our model we reanalysed these light curves. It appears that the "hot spot" hypothesis fits the observations relatively well, but the parameters of this active region estimated via the B and the V filters are significantly different. Although the system has a high degree of overcontact $(f_{\rm over} \sim 35\%)$, the obtained results show a large difference in the components' temperature ($\Delta T \sim 1000\ \rm K$),which is hard to explain. Besides, the analysis of our new observations presented in this paper indicates approximately equal temperatures and a much lower overcontact degree. So, the "hot spot" hypothesis is taken as unrealistic. We look for the solution in the hypothesis on dark spotted areas located on one of the system's components.

In this case the best fitting of the observations was achieved under the assumption of two spotted areas on the primary star, appearing at high latitudes on both hemispheres of the star. The results for system's basic parameters agree with the results of the analysis of our new observational material. This means that the high degree of asymmetry in Hoffmann's light curves, with much deeper primary minimum, can be completely explained by the presence of such active spotted regions.

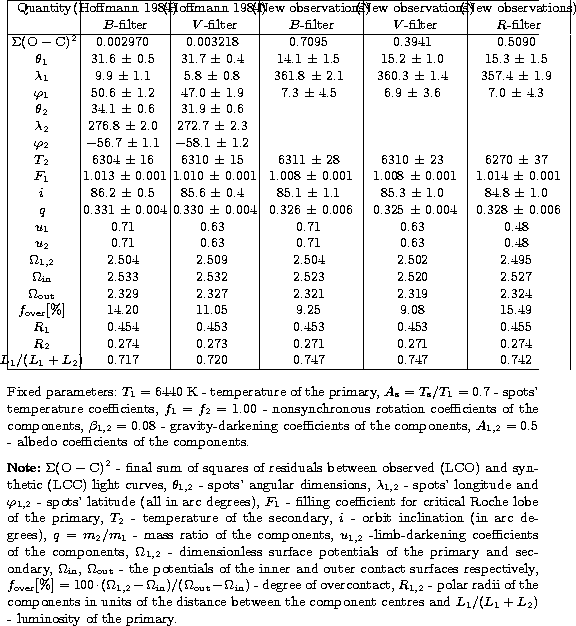
The parameters derived from the light curves analysis are listed in Table 2. The errors in parameter estimation originated from the nonlinear least-squares method which the inverse problem method is based on.

  

Table 2: Results of the analysis of the WZ Cep light curves obtained by solving the inverse problem for the Roche model with spotted areas on the primary component

Following from the inverse problem solutions for individual light curves, Fig. 1. (Left) presents the optimum fit of the observed light curves (LCO) by the synthetic ones (LCC). The light curves are normalised to the brightness at the orbital phase of 0.25. The final residuals (O-C) between the observed (LCO) and optimum synthetic (LCC) light curves are given, too. The right-hand column on these figures shows the view of the Roche models of the system WZ Cep, obtained with the parameters estimated by analysing the corresponding light curves. Thanks to such plots, one sees how would a CB system look like at a noted orbital phase, chosen so that the spots are visible.

It is evident from Table 2, and from Fig. 1 that Roche model with spotted areas on the primary component gives a very good fit of the Hoffmann's and our new light curves. For basic parameters of the system we have almost the same values. This indicates that the complex nature of the light curve variations between these two groups of observations is mainly caused by changes in the position and size of the spotted areas.

Figure 2 presents the optimum synthetic light curves (LCC) derived by analysing Hoffmann's and our observations (LCO) in the B and V passbands, drawn together. Since we do not have the data about the comparison star, which Hoffman used to give his differential magnitudes for WZ Cep, in this figure both sets of light curves are normalised to the primary maximum at the phase 0.25. In respect to this light level both sets of observations give quite the same depth of the secondary light-curve minimum (phase 0.5). Consequently, main variations between these two groups of light curves are in the depth of the primary minimum and in the height of the secondary maximum. Deeper primary minimum and lower secondary maximum in Hoffmann's observations can be explained by the location of spots, which at these orbital phases decrease the radiation flux coming to the observer. Such changes in the shape of light curves suggest considerably different levels of activity in the system WZ Cep during those two epochs of observations.

  

Figure 1: Left: Observed (LCO) and final synthetic (LCC) light curves of WZ Cep with final $\rm O-C$ residuals obtained by solving the inverse problem within the framework of the Roche model with spotted areas on the primary; right: The view of the Roche model for the WZ Cep at the corresponding orbital phase with parameters estimated by solving the inverse problem

  

Figure 2: Optimum synthetic (LCC) light curves derived by analysing Hoffmann's and our observations (LCO) in the B and V passbands, drawn together and changes of the colour-index, $\Delta$(B-V) and $\Delta$(V-R), with the orbital phase

This panel presents also the changes $\Delta(B-V)$ and $\Delta(V-R)$ of the colour indexes with the orbital phase. They are calculated from the best synthetic light curves (LCC) obtained by solving the inverse problem. In both groups of these light curves the changes of the colour-index, $\Delta(B-V)$, show the reddening around the primary minimum. In Hoffmann's light curves this effect is evident in the large part of the light curve. This reddening may be attributed to the spots' effects. The size of the spotted areas can be an indicator of the system's activity. The analysis of Hoffmann's light curve shows that spotted areas appear at high latitudes, near the polar regions on primary's both hemispheres, covering a significant part of the stellar surface. Their presence leads to a high asymmetry of the light curves. It is possible that a large spotted area near the stellar polar regions corresponds to an enhanced activity of the system. It seems that system's activity decreases after these observations. New light curves obtained during 1995 are almost symmetrical and their analysis gives a relatively small spot at lower latitude, near the neck between stars. At this point one can see that there are no certain differences between solutions for the B, V and R light curves.

Compared to "hot spot" hypothesis (Kaluzny 1986), these results show a much lower overcontact degree and approximately equal temperature of the components. The temperature of the secondary is approximately 140-170 K lower than the temperature of the primary. The variations of the orbit inclination, obtained by solving individual light curves, are within the accuracy limits of the evaluation of this parameter.