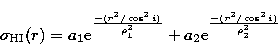
We have collected the maps of the integral HI density distribution in the catalogue of Paper I. As the main parameter of the sample we are dealing with is the real extension of the gas, we ought to make the deconvolution. Then, among these maps, we kept those whose contour lines show no detailed structures which would complicate a further analysis. In this way, we can apply a simplified gaussian model for the gas distribution that masks particular details, asymmetries and some large-scale features that are common in most galaxies.
It is known that the real HI distribution often shows a central
depression, especially in early spiral galaxies (Roberts 1975; Sersic
1980). It is convenient that the model representative of the gas
distribution takes this fact into account. A frequently-used symmetrical
model which gives a useful rough representation for most spiral galaxies
is the sum of two gaussians (Shostak 1978; Hewitt et al. 1983).
One gaussian distribution of HI gas may work for irregular galaxies, because
of their flat
gaseous disk distribution. Thus, we have adopted one and two gaussian
models of the HI distribution for irregular and spiral galaxies, respectively,
which are represented by the following expression:
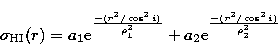 |
(1) |
In order to make the fit, we first determined the major axis of the gas distribution from the map. On this major axis, we obtained the radial distances (r) and the observed HI surface density at these distances. It is worth to noting that the HI major axis may not be coincident with the optical axis. In fact, this issue lead us to consider only the papers with maps of the total distribution of the gas emission, and reject those papers with observations along only one axis of the galaxy.
The expression (1) was convolved with the beam width of the telescope used in
the observation, which was supposed gaussian as well. This convolution
must reproduce the distribution of the HI surface density observed in the map.
Then, we iteratively vary ![]() in expression (1) until the best mean
least square fit between the calculated and observed values is achieved. With
respect to the relative strength of the gaussians, represented by the C1
parameter, we took its values at -0.6 or -0.3, depending on which gave
the best fit to the observations. The result was that for galaxies with
morphological type earlier than 4, the number of objects that best fit with
C1 = -0.3 is approximately the same as the one with C1 = -0.6.
However, for later-type galaxies, the number of best fits with C1 =
-0.3 is remarkably large. This result may be in agreement with the fact
that the central depression in the HI distribution seems to be less
pronounced in late-type systems, which possess small bulges.
in expression (1) until the best mean
least square fit between the calculated and observed values is achieved. With
respect to the relative strength of the gaussians, represented by the C1
parameter, we took its values at -0.6 or -0.3, depending on which gave
the best fit to the observations. The result was that for galaxies with
morphological type earlier than 4, the number of objects that best fit with
C1 = -0.3 is approximately the same as the one with C1 = -0.6.
However, for later-type galaxies, the number of best fits with C1 =
-0.3 is remarkably large. This result may be in agreement with the fact
that the central depression in the HI distribution seems to be less
pronounced in late-type systems, which possess small bulges.
For comparison with optical isophotal diameters, the best-fit model is used
to compute the HI isophotal diameter, then corrected by beam and inclination
effects. The isophotal diameters are defined according to a particular
isophote. By inspection of the data, we find that the best sensitivity reached
in the observations is, in most cases, 2.5 1019 at cm-2, and we have
adopted this value for estimating the HI isophotal diameter (![]() ).
We only kept those galaxies measured until a surface density less or equal
to 15 1019 at cm-2, because we have found that the extrapolation
is not valid for larger values.
).
We only kept those galaxies measured until a surface density less or equal
to 15 1019 at cm-2, because we have found that the extrapolation
is not valid for larger values.
In Table 1, we have listed the galaxies that make up the sample
that we use for the subsequent analysis.
The optical parameters are extracted from the LEDA catalogue
(Lyon-Meudon Extragalactic Database, first and second edition). First entries
to the table are:
Column 1: Galaxy name.
Column 2: Alternative name of the galaxy.
Column 3: Optical isophotal diameter measured to the surface brightness
level of 25 mg/[]'' corrected for galactic and internal absorption
(D0), in arc minutes.
Column 4: Morphological type.
Column 5: Inclination, in degrees.
Column 6: Distance, in Mpc. When the distance is uncertain, the extreme
assumed values are quoted. See following discussion.
Column 7: The linear diameter A(0) in kpc, from Cols. 3 and
6.
Column 8: HI mass, ![]() , in 109 M0. The adopted
values of
, in 109 M0. The adopted
values of ![]() are discussed in Sect. 4.
are discussed in Sect. 4.
Column 9: Mean apparent surface density of HI, ![]() , in
1021 at cm-2, from Cols. 7 and 8.
, in
1021 at cm-2, from Cols. 7 and 8.
Column 10: Mean real surface density, ![]() , in
1020 at cm-2, from Col. 8 and the HI isophotal diameter,
, in
1020 at cm-2, from Col. 8 and the HI isophotal diameter,
![]() (see Col. 3 of second entry).
(see Col. 3 of second entry).
Second entries to the Table are:
Column 1: Telescope used in the observation. (see Paper I for the
abbreviations).
Column 2: Beam width of the telescope, in arc minutes.
Column 3: Ratio between the HI and optical isophotal diameters,
![]() .
.
Column 4: References. The reference numbers are the same as those of the
catalogue of Paper I.
Copyright The European Southern Observatory (ESO)