![\begin{displaymath}
\sigma(r)= \mbox{ } \sigma_{0} \mbox{ } \exp \mbox{ } \left[ -\left( \frac{r}{r_{0}}\right) ^{n} \right],\end{displaymath}](/articles/aas/full/1998/10/ds7150/img16.gif)
In order to generate an extrapolated total t-system magnitude from a
low-resolution surface-brightness profile, Sérsic's (1968)
law is adopted:
![\begin{displaymath}
\sigma(r)= \mbox{ } \sigma_{0} \mbox{ } \exp \mbox{ } \left[ -\left( \frac{r}{r_{0}}\right) ^{n} \right],\end{displaymath}](/articles/aas/full/1998/10/ds7150/img16.gif) |
(5) |
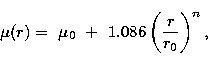 |
(6) |
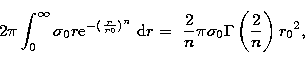 |
(7) |
Clearly, this generalisation incorporates not only the ![]() law
(
law
(![]() ) but also exponentials (n=1) and Gaussians (n=2) as
well as both intermediate and more extreme cases.
Although it is a one-component model, galaxies exhibiting two-component
(or yet more complicated) structure can be comfortably accommodated by this
scheme after their images have been smoothed sufficiently.
) but also exponentials (n=1) and Gaussians (n=2) as
well as both intermediate and more extreme cases.
Although it is a one-component model, galaxies exhibiting two-component
(or yet more complicated) structure can be comfortably accommodated by this
scheme after their images have been smoothed sufficiently.
For the benefit of readers wishing to use this extrapolation system, a
listing of the relevant FORTRAN code can be found in
Appendix A. The subroutine EXTRAPOL.FOR:
(1) increments the profile-curvature parameter n,
and attempts (for each n) to fit Sérsic's law to a surface-brightness profile defined by
elliptical isophotes (ri, ![]() (r),
(r), ![]() );
(2) quantifies the quality of the fit obtained for each value of n; and
(3) integrates the volume beneath the surface defined by the best-fitting
profile form (after rotation through 2
);
(2) quantifies the quality of the fit obtained for each value of n; and
(3) integrates the volume beneath the surface defined by the best-fitting
profile form (after rotation through 2![]() radians about r=0) to
radians about r=0) to ![]() ,
thereby yielding a total-magnitude estimate.
It calls the subroutine FIT and the function
GAMMLN, both from Press et al. (1986). Note that
FIT actually fits a straight line of the form Y=A+BX, not one
of the form Y=AX+B. Also, in order to reduce the dependence on other
subroutines and functions, we removed the lines:
,
thereby yielding a total-magnitude estimate.
It calls the subroutine FIT and the function
GAMMLN, both from Press et al. (1986). Note that
FIT actually fits a straight line of the form Y=A+BX, not one
of the form Y=AX+B. Also, in order to reduce the dependence on other
subroutines and functions, we removed the lines:
Q=1. and
Q=GAMMQ(0.5![]() (NDATA-2),0.5
(NDATA-2),0.5![]() CHI2),
CHI2),
from this subroutine and removed the parameter
Q from Line 1.
Although t-system total magnitudes cannot generally be derived directly
from high resolution surface photometry of bright galaxies in the
literature, they can be derived from surface photometry of virtually all
galaxies fainter than ![]() mag provided that the resolution
of the photometry (after smoothing) is coarser than about
mag provided that the resolution
of the photometry (after smoothing) is coarser than about ![]() (FWHM).
In the compilation of their VPC, Young & Currie (1998) found that a reasonable amount
of smoothing of their plate-scan data was necessary simply in order to prevent the fragmentation of images during the
image segmentation process. They found that the minimum degree of smoothing required by the
segmentation software was actually sufficient for the derivation of t-sytem total magnitudes from
the surface-brightness profiles of all unsaturated galaxies with enough isophotes above the
limiting one for the fits to be performed.
(FWHM).
In the compilation of their VPC, Young & Currie (1998) found that a reasonable amount
of smoothing of their plate-scan data was necessary simply in order to prevent the fragmentation of images during the
image segmentation process. They found that the minimum degree of smoothing required by the
segmentation software was actually sufficient for the derivation of t-sytem total magnitudes from
the surface-brightness profiles of all unsaturated galaxies with enough isophotes above the
limiting one for the fits to be performed.
Copyright The European Southern Observatory (ESO)