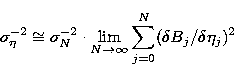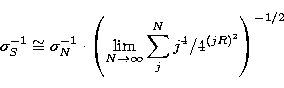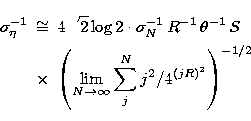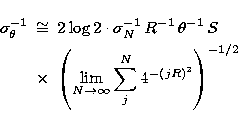Up: A CO() and ()
The derivation of estimates for the uncertainties in flux S,
position 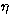 , and width
, and width 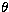 of a one-dimensional gaussian
brightness distribution centered at
of a one-dimensional gaussian
brightness distribution centered at 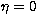 and sampled at
locations
and sampled at
locations 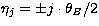 (
(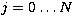 ,
,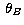 is the
beamwidth) with additive noise
is the
beamwidth) with additive noise 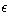 of zero
mean and variance
of zero
mean and variance 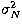
| 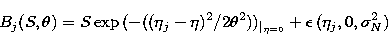 |
(8) |
requires the use of non-linear regression. A Gaussian profile is indeed
non-linear in 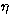 and
and 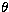 according to
according to
| 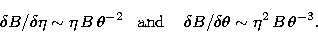 |
(9) |
Though non-linear regression is required to derive estimates of the
uncertainties in S, 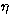 and
and 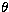 , we used an approach
suggested by the iterative Gauss-Newton method (Bates & Watts 1988)
to derive a linear approximation to these estimates in the limit of
high signal-to-noise (
, we used an approach
suggested by the iterative Gauss-Newton method (Bates & Watts 1988)
to derive a linear approximation to these estimates in the limit of
high signal-to-noise (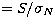 ). In this case the one sigma
confidence limit for the position
). In this case the one sigma
confidence limit for the position 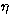 in the limit of high N can
be written to
in the limit of high N can
be written to
| 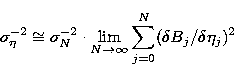 |
(10) |
with similar expressions for 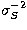 and
and 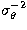 .According to equation (10) the uncertainties in S,
.According to equation (10) the uncertainties in S, 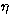 and
and 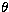 for the gaussian brightness distribution B are given by
for the gaussian brightness distribution B are given by
| 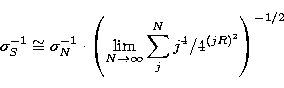 |
(11) |
| 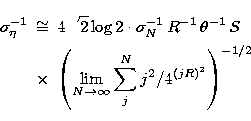 |
|
| (12) |
| 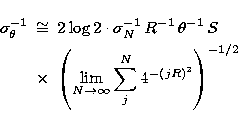 |
|
| (13) |
where 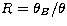 . Note that in the R=1 limit (i.e. an
unresolved object) the uncertainties can roughly be estimated to
. Note that in the R=1 limit (i.e. an
unresolved object) the uncertainties can roughly be estimated to
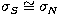 ,
, 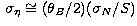 and
and 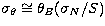 . The errors in the estimates are reasonably small for
samples with snr
. The errors in the estimates are reasonably small for
samples with snr 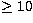 . In analogy, statistical estimates for S,
. In analogy, statistical estimates for S,
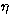 and
and 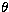 according to the two-dimensional case were
approximated to
according to the two-dimensional case were
approximated to 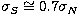 ,
, 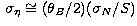 and
and 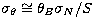 and found to be
better than 20% for data with snr
and found to be
better than 20% for data with snr 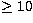 .
.


Up: A CO() and ()
Copyright The European Southern Observatory (ESO)
![]() and
and ![]() , we used an approach
suggested by the iterative Gauss-Newton method (Bates & Watts 1988)
to derive a linear approximation to these estimates in the limit of
high signal-to-noise (
, we used an approach
suggested by the iterative Gauss-Newton method (Bates & Watts 1988)
to derive a linear approximation to these estimates in the limit of
high signal-to-noise (![]() ). In this case the one sigma
confidence limit for the position
). In this case the one sigma
confidence limit for the position ![]() in the limit of high N can
be written to
in the limit of high N can
be written to