1. Input physics and population II models

As a starting point we will assume as a reference frame (step 1) the evolutionary scenario presented by Straniero & Chieffi (1991) and by Castellani et al. (1991: hereinafter CCP), which covers with a homogeneous set of computations the major evolutionary phases experienced by galactic globular cluster stars. As a relevant point, let us here recall that the above evolutionary scenario appears in excellent agreement with computations based on similar physics given by Sweigart (1987); in particular theoretical predictions concerning the mass of the He core at the He ignition agree to within few thousandths of solar mass.

The "step 1" column in Table 1 (click here) gives details of the relevant physics adopted in those models which now can be improved.

 

Step 1 2 3 4 5 6 7 8

EOS Str88 Str88 Str88 OPAL OPAL OPAL OPAL OPAL

OPAC LAOL OPAL OPAL OPAL OPAL OPAL OPAL OPAL

OPAC-CO LAOL LAOL OPAL OPAL OPAL OPAL OPAL OPAL

Fow75 Fow75 Fow75 Fow75 Cau88 Cau88 Cau88 Cau88

NEU Mun85 Mun85 Mun85 Mun85 Mun85 Haft94 Mun85 Haft94

0.384 0.382 0.382 0.411 - - 0.410 0.410

13.62 13.50 13.50 11.58 - - 11.58 11.58

3.245 3.279 3.279 3.275 - - 3.291 3.322

15.28 15.17 15.17 13.06 - - 13.22 13.22

0.5054 0.5098 0.5098 0.5054 0.5054 0.5054 0.5092 0.5152

0.238 0.238 0.238 0.238 0.238 0.238 0.238 0.238

1.617 1.635 1.635 1.656 1.663 1.663 - 1.666

3.976 3.991 3.990 3.983 3.974 3.974 - 4.010

96.97 93.71 87.17 87.65 80.44 80.28 - 75.02

 

Top to bottom one finds:
- Equation of State (EOS) Str88: Straniero (1988) implemented at the lower temperature with Saha equation.
- Radiative Opacity for H, He mixtures (OPAC). LAOL: Los Alamos Opacity Library (Huebner et al. 1977) implemented at the lower temperature with Cox & Tabor (1976) opacity tables.
- Radiative Opacity for C, O mixtures (OPAC-CO). LAOL: Los Alamos Opacity Library (Huebner et al. 1977).
- He burning rates (-rates). Fow75: Fowler et al. (1975); Harris et al. (1983); Caughlan et al. (1985).
- Neutrino energy losses (NEU). Mun85: Beaudet et al. (1967); Munakata et al. (1985); Richardson et al. (1982).

The updating of the input physics runs as follows:

- EOS from Str88 to OPAL (Rogers 1994; Rogers et al. 1996), implemented in the temperature-density region not covered by OPAL with Str88, plus Saha EOS in the outer stellar layers. The transition from OPAL to other EOS appears smooth and without discontinuities.

- OPAC and OPAC-CO from LAOL to OPAL (Rogers & Iglesias 1992; Iglesias & Rogers 1996),

- -rates from Fow75 to Cau88 (Caughlan & Fowler 1988) and, finally,

- NEU from Mun85 to Haft94 (Haft et al. 1994) for plasma neutrino production and Itoh et al. (1996) for the other kinds of neutrino energy losses.

Electron screening (Graboske et al. 1973; DeWitt et al. 1973) and electron conductivity (Itoh et al. 1983) have not been subject to relevant improvements since that time. As a matter of fact, numerical experiments performed with our code show that neither improvements in strong electron screening, as given by Itoh et al. (1977) and Itoh et al. (1979), nor the alternative approach to weak and intermediate screening (Mitler 1977) affect the evolutionary phases we are dealing with.

Table 1 (click here) gives a list of the various modifications in the input physics together with the corresponding values for selected evolutionary quantities. The upper portion of the table gives the steps in updating the physics inputs, whereas in the lower portion of Table 1 (click here) one finds selected results concerning the H burning phase of a 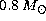model 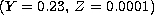and the He burning phase of the same model but assuming the original mass reduced to 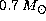by mass loss. Top to bottom one finds: the luminosity (Log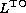) and the age of the 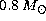H burning model at the track Turn Off (TO), the luminosity (Log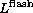), the age (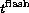) and the mass (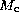) of the He core at the He flash and the surface helium abundance () after the first dredge-up. For the He burning 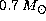one finally finds the Zero Age Horizontal Branch luminosity (Log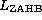), and effective temperature (Log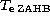) together with the time spent in the central He burning phase as a Horizontal Branch (HB) star. Luminosities and masses are in solar units throughout.

Even a quick inspection of results in Table 1 (click here) shows the relevant effects produced by the OPAL-EOS on the MS lifetimes and TO-luminosities, an occurrence already well discussed in the literature (see, e.g., Chaboyer & Kim 1995). For HB models, one finds that improvements in the opacity of H-rich mixtures have the major effect of moderately increasing the HB luminosity (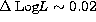) and decreasing the HB lifetime by 3.4%. As expected, CO opacity affects only the advanced phases of central He burning, decreasing the HB lifetimes by a further 7%. As a whole, one finds that the major effect of the new opacities is the decrease of HB lifetimes by the not negligible amount of about 10%. Step 4 in Table 1 (click here) shows that the passing from the previous EOS to the more recent OPAL EOS does not affect HB lifetimes; however one finds that the HB luminosity increases by a further , in spite of the of the small decreases in 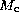, whereas the age of the flashing RG decreases by about 2 Gyr.

Steps 5, 6, 7 and 8 finally report the effect of improved evaluations of the triple nuclear reactions and of the plasma neutrino energy loss rates. On very general ground, one expects that both these mechanisms affect the He ignition at the flash, affecting in turn the structure of the initial ZAHB models. To disentangle this effect from the effect on the physics of HB models, step 5 and 6 concern only ZAHB models, introducing the new rates for 3 reactions (Caughlan & Fowler 1988) and for plasma neutrino production (Haft et al. 1994) in two subsequent steps for the fixed value of the ZAHB Helium core mass given by the result of step 4. One finds that the new 3 rates further increase, though slightly, the HB luminosity, whereas HB lifetimes are again substantially decreased by a further 8%. On the contrary, one finds that HB structures are only marginally affected by the NEU treatment, as predicted earlier (Gross 1973).

Step 7 shows the effect of new 3 rates on H burning models as HB progenitors. Finally, step 8 gives the results for our "best" models where all the available updating of the physics have been taken into account. Due to the effect of both 3 rates and NEU, the He flash is delayed and the peak luminosity of the RG structures is increased, becoming about 0.2 mag brighter than in Straniero & Chieffi (1991; step 1 in Table 1 (click here)). Correspondingly the value of 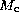"jumps" from 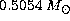to 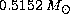, contributing to a further increase of the HB luminosity. From data in Table 1 (click here), one recognizes that 3 rates and NEU give a similar contribution to the quoted increase of 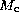. As a whole, one finds that passing from CCP to present best models the major modifications concerning HB evolution are given by the increase of the ZAHB luminosity by about 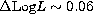( 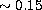mag) and by the decrease of HB lifetimes by the huge amount of, about, 23%. As one can easily understand, and as we will discuss later on, this will have rather dramatic effects on current calibration of the R parameter.

To orientate the reader in the current literature, let us review available theoretical estimates in terms of the quoted physical scenarios. As a starting point, let us notice that CCP computations adopt more or less the same input physics adopted in previous computations (as, e.g., Sweigart 1987; Dorman & VandenBerg 1989; Lee & Demarque 1990). Dorman (1992) adopts neutrino energy losses and opacities as in CCP, improving nuclear reactions rates as in Caughlan & Fowler (1988) but taking the EOS from Eggleton et al. (1973). Dorman et al. (1993) adopt the same inputs as Dorman (1992), but low-temperature opacities from Alexander (1975). Mazzitelli et al. (1995) have OPAL EOS and opacity, but using Dappen et al. (1988) EOS in H burning models (as stated in D'Antona et al. 1997, who updated the turn off models with OPAL EOS); nuclear reactions rates are from Harris et al. (1983) and neutrinos from Itoh et al. (1989). Salaris et al. (1997) models overlap present step 4 assumptions. As a result, one finds that our step 8 is till now the first one including all available updating of the input physics. According to such an evidence, in the following section we will investigate the evolutionary behavior of similar models, discussing the calibration of the most relevant evolutionary parameters.