In order to obtain an analytical least-squares solution we use the
simplified rotated echelle relation. The residual 
of a given line of index 
at position
(xi,yi) and of wavelength 
, and the relative order
number pi, is given by
One has to consider the case where the order number m is
also an unknown quantity since it has useful practical applications.
We rewrite, using 
By determining the partial derivatives
of Ri2 with respect to each parameter (m,a,b,c) we obtain
a system of the form A x = B with A a 
matrix and B a
vector such as
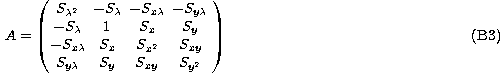
with the quantities Sx, etc... being defined as
and similar formulae for Sy, 
,
, 
, 
,
, Sy2, 
, 
,
.
The full system was solved using mathematical packages, and solutions for subsets with fixed parameters were determined with a view towards robust techniques for practical calibration procedures.