4. Instrumental polarization at the Cassegrain
focus

4.1. Reflection geometry for hyperbolic secondary

The secondary mirror is a convex hyperboloid, which can be represented by the following equation:

The above equation represents two branches of hyperboloid along the Z-axis. However, the one towards the positive direction of Z-axis will represent the secondary mirror in our case. In Eq. (23)

where e is the eccentricity of the hyperboloid, is the distance between the two branches of hyperboloid (vertex-vertex), dd is the distance of the vertex of secondary mirror from the origin (which is the vertex of paraboloid also). The quantities c and dd can be found out easily once we know the diameters of two mirrors (h1 and h2), beam sizes (f1 and f2) at the two focii and eccentricity of the hyperbolic surfaces (e).

Now the equation of the ray reflected from the primary mirror (which is same as the ray incident on the secondary mirror) can be written as

The expressions for are given in Eq. (5). Now substituting in (23) we get

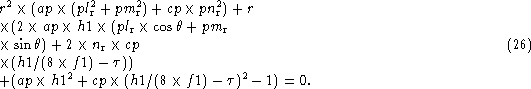
This Eq. (26) has two roots for r and we shall accept only that root (say r= rt ) which corresponds to the hyperboloid of our choice (i.e. the secondary mirror).

In this process we determine the point of incidence (xs,ys,zs) on the secondary mirror as the following:

Now the d.c. of the normal at the above point of incidence on to the secondary can be given by

Now, as we derived in the case of primary paraboloid earlier, in the present the angle of incidence si, d.c. of reflected ray , the d.c. of the vectors ss , spi (sl_pi, sm_pi, sn_pi) , spr (sl_pr, sm_pr, sn_pr) can also be derived as (pl. see Sect. 2):

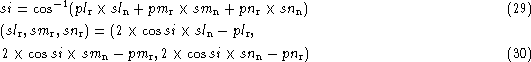
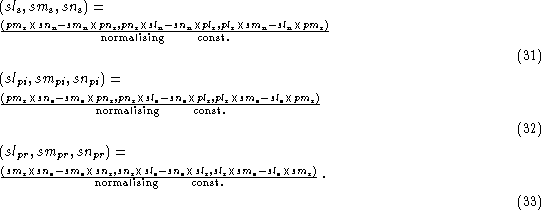
We are now in a position to calculate the reflectivities for the p and s components of the electric vector ( and ) for reflection on the secondary mirror. For the ray reflected from the primary mirror we have the and amplitude components. Again taking their components in the (sl_pi, sm_pi, sn_pi) and (sl_s, sm_s, sn_s) directions, we get the amplitudes (, ) for the incident ray on the secondary in the p and s directions. Multiplying them by the reflectivities for the secondary mirror, we get the reflected amplitudes and for the secondary mirror. Now to calculate instrumental polarization, we shall consider two cases (i) when rays incident on the primary are completely unpolarized and (ii) when rays incident on the primary are polarized.

4.2. Case of unpolarized rays incident on primary

Each individual ray, which is initially unpolarized after reflection from primary will get polarized (say, with degree of polarzation pp). This ray is now incident on the secondary and it consists of two parts unpolarized and polarized maintaining a ratio (1-pp) : pp, in their intensities. For the unpolarized part to calculate the stokes parameters we follow the same proceedure as was done in case of primary mirror (assuming ). For polarized part we calculate the Stokes parameters in a similar way but the Stokes parameter will no longer be assumed to be zero.

The two sets of Stokes parameters will now be added to calculate the instrumental polarization for a particular ray (reflection geometry) and then transformed into the XY-frame. Integrating all these Stokes parameter values for different rays (within range , we get the resultant Stokes parameter values. These values will finally help us to calculate instrumental polarization by using Eqs. (15a,b) at the Cassegrain focus, for unpolarized light incident on primary.

4.3. Case of polarized rays incident on primary

When light is totally polarized and incident on primary mirror, we first calculate the reflected components and on the primary. We take their components in the directions (sl_pi, sm_pi, sn_pi) and to get the p and s components of incident ray on the secondary. From this we get the p and s components of reflected amplitudes ( and ) on the secondary. These amplitudes help us to calculate the Stokes parameters in the local (p-s) frame of secondary and these are later transformed into the (X-Y) frame. These set of Stokes parameter values are used to calculate the observed polarization values, as was done in Sect. 3.2.